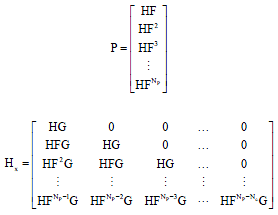
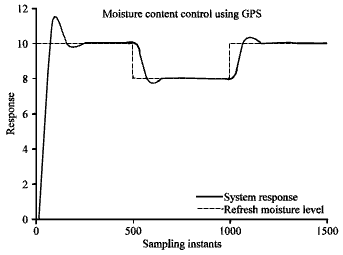
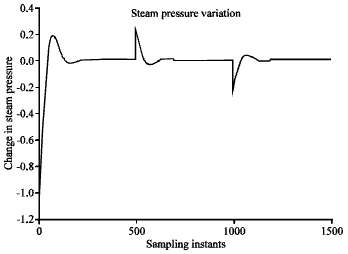
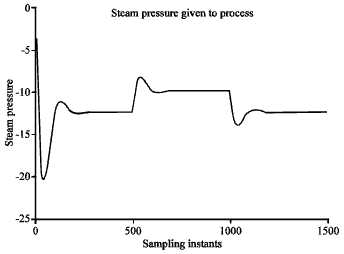
Research Article
Design and Analysis of Generalized Predictive Control for Moisture Content Control in a Benchmark Paper Plant
School of Electrical and Electronics Engineering, SASTRA University, 613 401, India
N. Muthukumar
School of Electrical and Electronics Engineering, SASTRA University, 613 401, India
K. Ramkumar
School of Electrical and Electronics Engineering, SASTRA University, 613 401, India
G. Balasubramanian
School of Electrical and Electronics Engineering, SASTRA University, 613 401, India