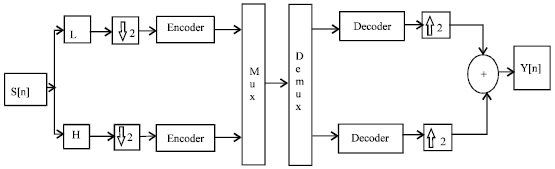
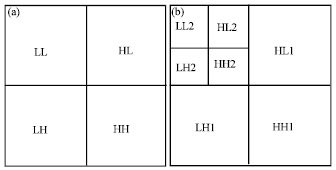
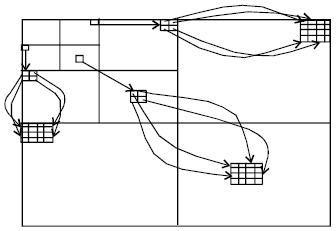
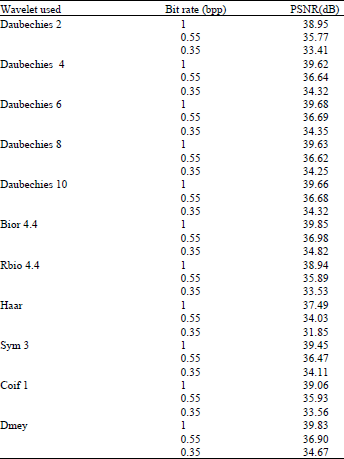
Research Article
Evaluation of Wavelet Filters in Image Coding Using SPIHT
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, 613401, Tamil Nadu, India
P.V.M. Vijayabhaskar
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, 613401, Tamil Nadu, India
G. Shiva
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, 613401, Tamil Nadu, India
P. Mithun
Department of Electronics and Communication Engineering, School of Electrical and Electronics Engineering, SASTRA University, 613401, Tamil Nadu, India