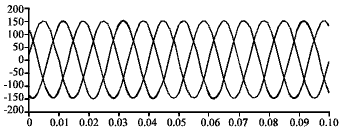
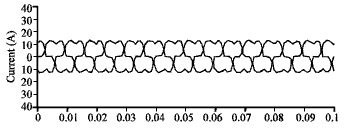
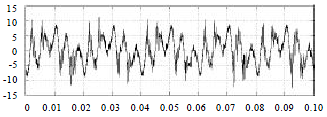
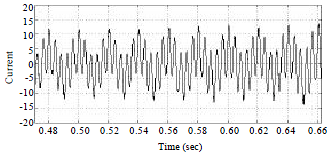
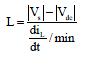Research Article
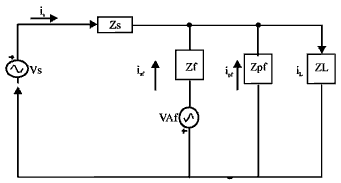
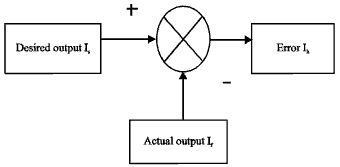
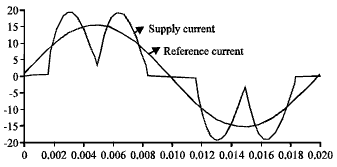
LMS Algorithm Based Fundamental Current Detection for Shunt Hybrid Filter
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
S. Jayalalitha
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India