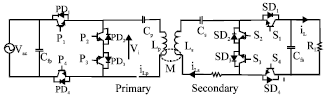
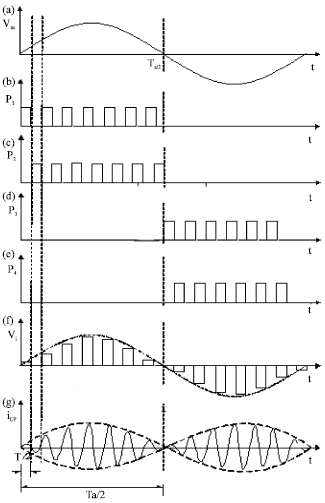
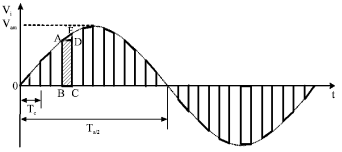
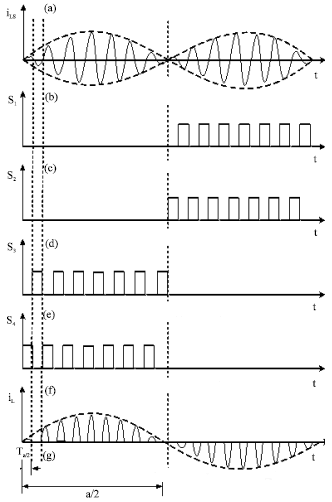
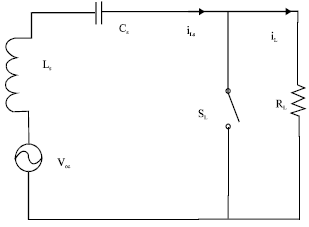
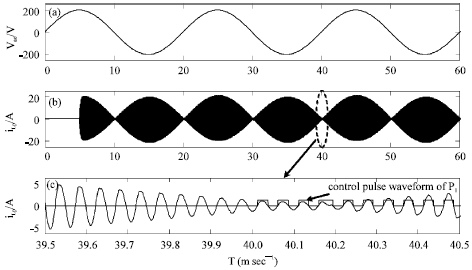
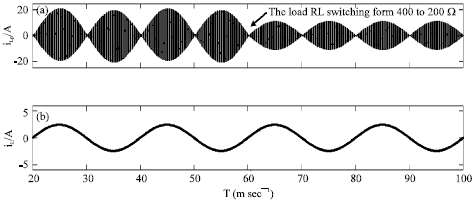
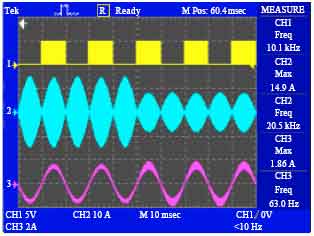
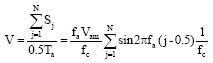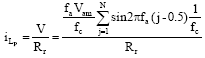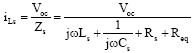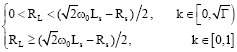Research Article
Research of the Constant Current Characteristic of Symmetric AC-AC Inductive Coupled Power Transfer System
College of Automation, Chongqing University, 400030, Chongqing, China
Yue Sun
College of Automation, Chongqing University, 400030, Chongqing, China
Zhihui Wang
College of Automation, Chongqing University, 400030, Chongqing, China
Chunsen Tang
College of Automation, Chongqing University, 400030, Chongqing, China