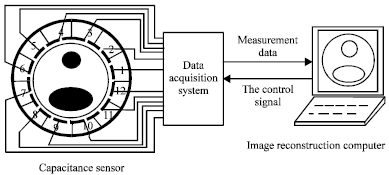
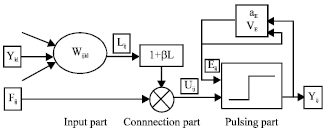
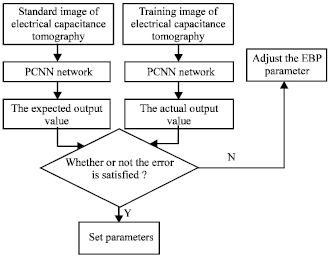
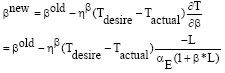Research Article
A Novel Image Reconstruction Algorithm Based on Pulse Coupled Neural Network for Electrical Capacitance Tomography System
Higher Educational Key Laboratory for Measuring, Control Technology, Instrumentations of Heilongjiang Province, School of Computer Science and Technology, Harbin University of Science and Technology, 150080, Harbin, People`s Republic of China
Chen Deyun
Higher Educational Key Laboratory for Measuring, Control Technology, Instrumentations of Heilongjiang Province, School of Computer Science and Technology, Harbin University of Science and Technology, 150080, Harbin, People`s Republic of China
Gao Ming
Higher Educational Key Laboratory for Measuring, Control Technology, Instrumentations of Heilongjiang Province, School of Computer Science and Technology, Harbin University of Science and Technology, 150080, Harbin, People`s Republic of China
Wang Lili
Higher Educational Key Laboratory for Measuring, Control Technology, Instrumentations of Heilongjiang Province, School of Computer Science and Technology, Harbin University of Science and Technology, 150080, Harbin, People`s Republic of China
Chen Yu
Higher Educational Key Laboratory for Measuring, Control Technology, Instrumentations of Heilongjiang Province, School of Computer Science and Technology, Harbin University of Science and Technology, 150080, Harbin, People`s Republic of China
Yu Xiaoyang
Higher Educational Key Laboratory for Measuring, Control Technology, Instrumentations of Heilongjiang Province, School of Computer Science and Technology, Harbin University of Science and Technology, 150080, Harbin, People`s Republic of China