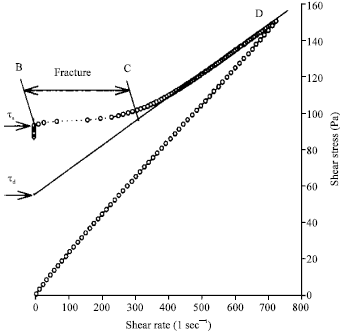
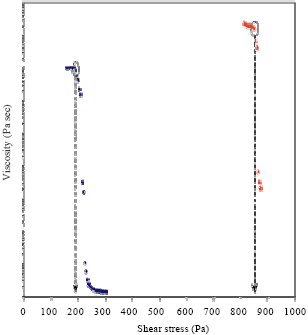
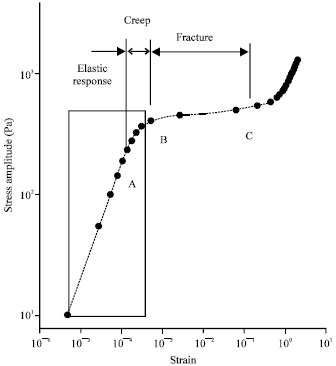
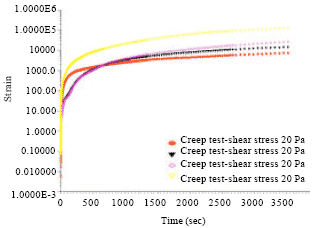
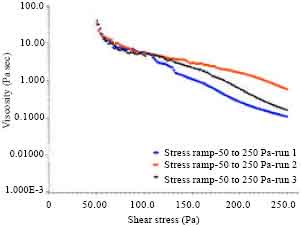
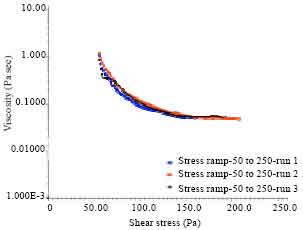
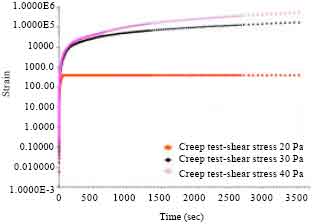
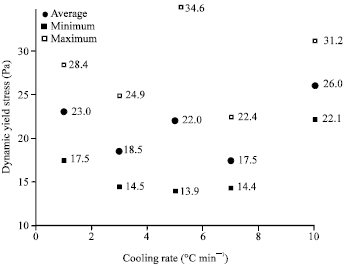
Research Article
Yield Stress Measurements of Waxy Crude Oil
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia
Azuraien Jaafar
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia