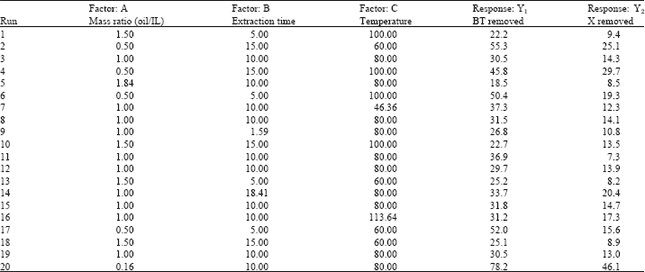
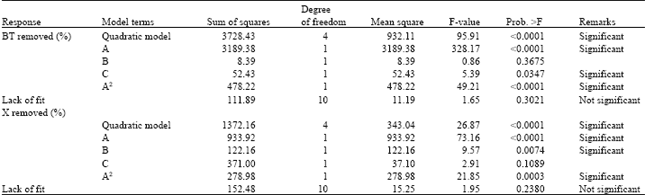
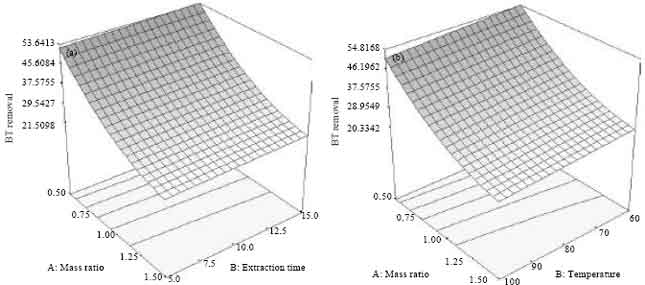
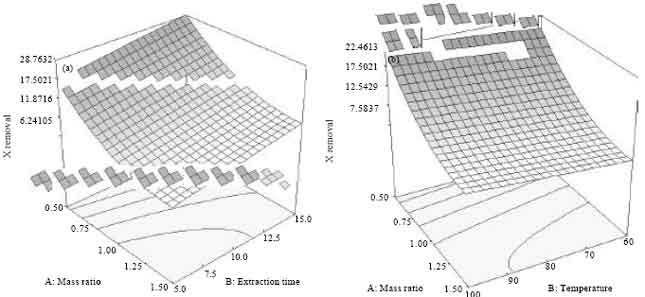
Research Article
An Optimization Study via Response Surface Methodology in Extracting of Benzothiophene and Xylene from n-C12 using 1-Hexyl-3-Methylimidazolium Tetrafluoroborate Ionic Liquid
Oil and Gas Technology Group, Faculty of Chemical and Natural Resources Engineering, Universiti Malaysia Pahang, Lebuhraya Tun Razak, Gambang, 26300, Pahang, Malaysia
Z. Man
PETRONAS Ionic Liquid Centre, Department of Chemical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia
M.A. Bustam
PETRONAS Ionic Liquid Centre, Department of Chemical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Tronoh, 31750, Perak, Malaysia