INTRODUCTION

Delta sigma modulation with cascaded stages have been proposed (Gothenberg and Tenhunen, 2002; Al-Taweel, 2006). This approach uses digital correction. Sensitivity of OTAs adaptation circuits used in high precession analogue design would be reduced by careful design of the modulator architecture.

Achieving high resolution and large bandwidth is accomplished using high-order adaptive sigma delta modulators. The slope-overload distortion for any varying input signal, the higher-order noise shaping function was realized using cascaded second order SDM. These circuits are sensitive to analog circuit imperfections, a good matching between the digital output and the analog filter. A prominent problem of the design of cascaded delta sigma modulation is the leakage of the quantization noise (Al-Taweel, 2006; Kiss, 1999). At last, the noise leakage can be reduced in the analog or digital estimation circuit design (Jose, 2010; Zouari et al., 2007).

Sigma delta quantizes estimate differently the quantization error of the first stage which is quantized by multi bit second stage. Also this modulator requires mismatch-shaping DAC in the first stage. Cancelation of the imperfect error causes the leakage of the quantization noise. To decrease this leakage, delta sigma modulation with second order cascaded stages are used. In the first stage of this scheme, 1-1.5 bit is applied whereas, 8-12 bit is applied in the second stage. Also, an adaptive digital FIR filter is applied in this scheme (Hawksford, 2005; Rombouts et al., 2003; Al-Taweel, 2010; Cauwenberghs and Temes, 2000).

This proposal consists of second order ASDM as shown in Fig. 1. The forth-order (2-2) cascaded modulator. Adaptive quantization with backward estimation is used in all sections. This can be obtained by feedback the encoded output signal adaptatively. As a result, the quantized input signal amplitude is estimated continuously, with low OSR of 16, as shown in Fig. 2. The output pulse of encoded signal feedback through adaptation scheme which consists of low pass filter followed by rectifier (OTAs) with variable voltage gain to continuously estimating the amplitude of sampling at every moment (Time varying the step size) to eliminate the varying input signal. If the input signal X(n) is rapidly increasing or decreasing, the output encoded pulses Y(n) are all 1s or all Os. Therefore the magnitude of the filter output will be relatively large. This will control the amount of the amplifier bias current which will vary the trans conductance (g_m), then the voltage gain of the amplifier (A_v) which means time varying step size Δ(n), (Al-Taweel, 2006).

In this study, a cascaded second order ADSM system is presented. In this approach, utilizing, adaptive quantization estimation and adaptive prediction estimation are used. High Operational Transconductance Amplifier (OTA) included higher gain, enhanced performance and better sensitivity for the cascaded structure than normal ADSM is proposed. Our method achieves continuous time varying step size and high SQNR with oversampling ratios. Simulation results show the illustration of the effect of linearity error quantization path for the cascaded structures.

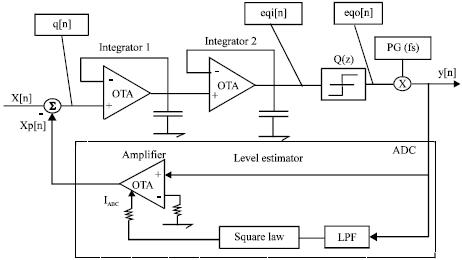Fig. 1:	Second order ASDM section

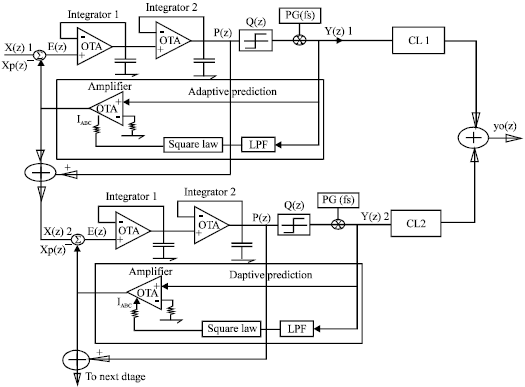Fig. 2:	Proposed cascaded two stages second order ASDMs scheme

OVERSAMPLING ADCS

The ADC is suitable for high resolution low-speed application, such as audio signal (0,3-3.4) KHz where the conversion speed is less than 0,3 KHz. For higher conversion speed 100-150 MHZ, the sigma delta ADC is suitable and the resolution is approximately 10-12 bit. So, the Nyquist rates ADCs are fast and flash ADC.

Oversampling improves the resolution obtained from a general Nyquist rate converter by using higher sampling frequency (fs>>2f_m), where oversampling ratio is defined as the ratio between the sampling frequency and the Nyquist frequency. So, if the samples occur often enough, the original waveform can be completely recovered from the sample sequence without fold over distortion by a low-pass filter. therefore the quantization noise power of an ADC can be reduced by factor of OSR, (OSR = fs/2f_m>>1) and for the maximum SNR there is a tradeoff between accuracy (N) and bandwidth (2f_B), Typically oversampling ratio ranges between 8 and 128.

SIMULATED QUANTIZATION NOISE

The quantization noise is calculated as a function of signal amplitude for a coder with uniform quantization intervals. The quantization error is created by digitizing an analog signal and is expressed as an average signal power to average noise power, so, the quantization error sequence q(n), is limited to ±Δ/2 and the quantization interval implying a uniform probability density of amplitude 1/Δ (Limketkai and Victor, 2000; Ziemer and Tranter, 1995). The digital quantizer output y(n) is fed back through DAC which is converted back into an analog discrete time signal X(n). So, the quantization error sequence q (n) is:

(1)

(2)

where, e_qi and e_qo are the input and output quantizer, the a mplitude of the quantization error for the resolution N = 4 bits:

(3)

where, A is the peak amplitude of the input sin wave signals. According to the entire signal-to-noise quantization the ratio is given as:

(4)

Substituting the total number of intervals into Eq. 4 produce the performance equation SNR as follows:

(5)

where, A_max is the maximum non overloaded amplitude, it's noted from Eq. 5 there is a relationship between the resolution N and its SNR performance in dB (Kiss, 1999; Jose, 2010).

In this study, cascaded two stages second order is introduced. Each stage converts the quantization error of the previous stage, then using the output of each stage to construct the output signal with little quantization errors of all stages as shown in Fig. 3.

The noise shaping can be achieved by recombination, the output of each stage of Fig. 2.

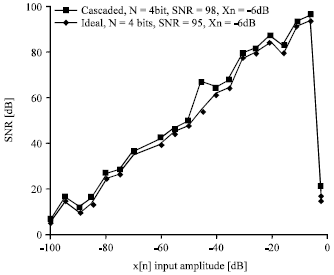Fig. 3:	Comparative SNR performance of the2-O ASDM and cascaded 2-O ASDM

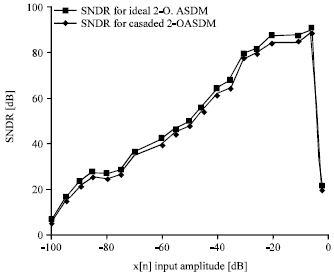Fig. 4:	SNDR as a function of input amplitude

Single-bit ADC is employed in the first second order stage and four bits ADC is employed in the lower resolution to improve the dynamic range, where the dynamic range is the ratio of the maximum amplitude signal to minimum amplitude signal, therefore, the ideal dynamic range is 30 dB. SNDR as a function of input amplitude is shown in Fig. 4.

Simulation shows that the maximum signal-to-quantization noise ratio for the cascaded structure achieved with higher performance and greater dynamic range (Ziemer and Tranter, 1995; Bellamy, 2000):

(6)

(7)

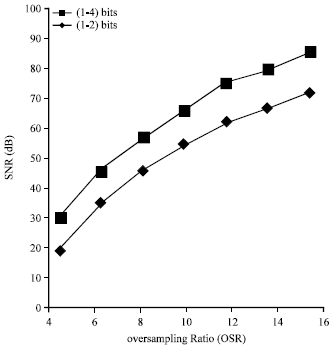Fig. 5:	SNR vs. oversampling ratio for fourth order cascaded ASDM

Using Eq. 5 or 6 the simulated SNR versus the oversampling ratio for fourth order cascaded shown in Fig. 5.