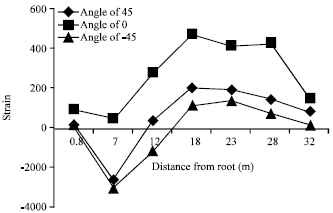
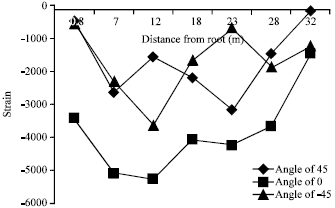
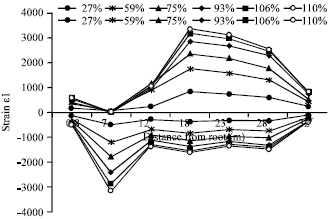
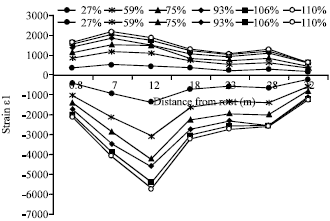
Research Article
Experimental Research for MW Wind Turbine Blade
Division of Mechanics, Nanjing University of Technology, Nanjing, China
Song Lin-Hui
Division of Mechanics, Nanjing University of Technology, Nanjing, China
He Bin
Division of Mechanics, Nanjing University of Technology, Nanjing, China
Fan Qin-Shan
Division of Mechanics, Nanjing University of Technology, Nanjing, China