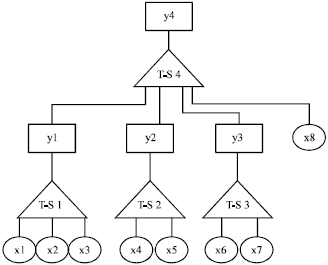
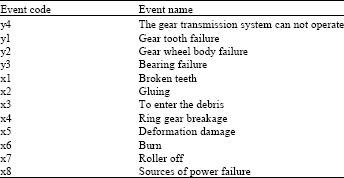
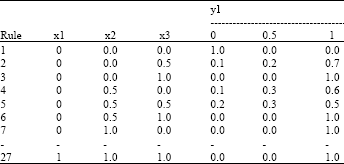
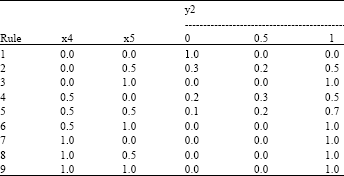
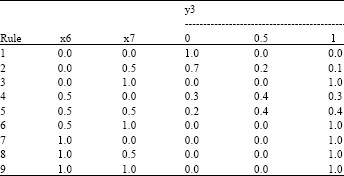
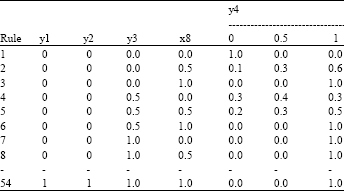
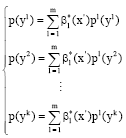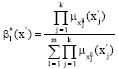Research Article
Search Method for Wind Turbine Gearbox Failures Based on Grey and Fuzzy Fault Tree Analysis
School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
Li Chengwei
School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
Sun Xiaogang
School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China