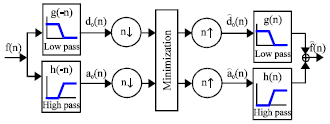
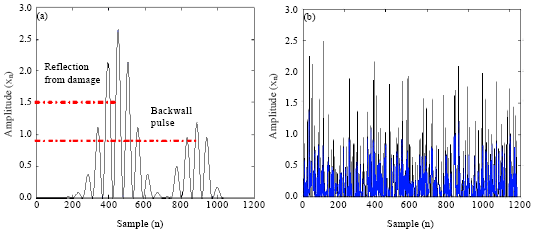
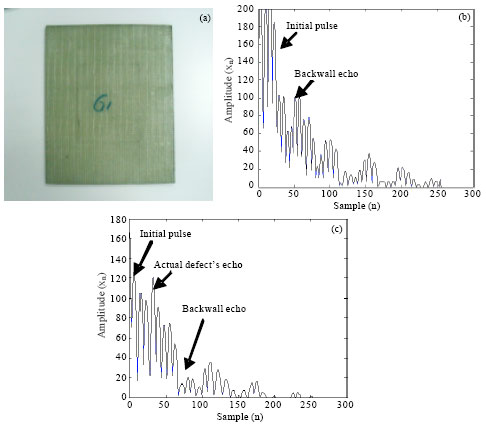
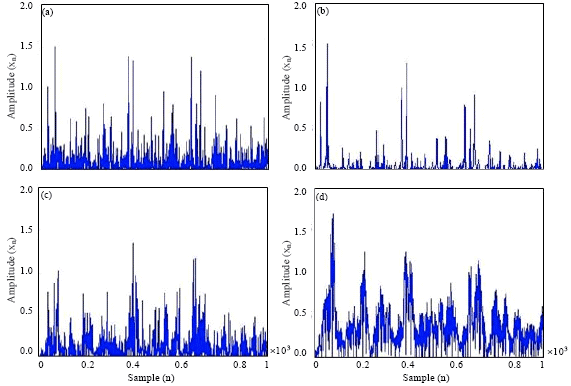
Research Article
Ultrasonic NDE for Internal Defect Detection in Multi-layered Composite Materials by Multi-resolution Signal Decomposition
Intelligent System and Robotic Laboratory, Institute of Advanced Technology, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
N. Ismail
Intelligent System and Robotic Laboratory, Institute of Advanced Technology, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Aidy Ali
Intelligent System and Robotic Laboratory, Institute of Advanced Technology, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Barkawi Sahari
Intelligent System and Robotic Laboratory, Institute of Advanced Technology, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
J.M. Yusof
Department of Mechanical and Manufacturing Engineering, Faculty of Engineering, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia