Research Article
Research on Continuous Double Auction Strategy in the Weak Efficient Markets
School of Management, Huazhong University of Science and Technology, Luoyu road 1037, Wuhan, China
According to Fama’s (Fama, 1965) definition for "weak efficient markets", if all prices are able to fully reflect the information contained in a historical price sequence for a continuous auction market, meaning the historical information can fully reflect the current market price, then no arbitrage opportunities will be left untapped and this market is considered a weak market.
Concerning research to verify whether continuous auction markets exist or not, there are primarily two foci: first, the verification of random walk and second the affective relationship between random walk and weak markets. In regard to the former, Dickey and Fuller (1979, 1981) put forward the well-known DF method to verify the random walk which Chinese scholars Fan and Zhang (1998) used to investigate stocks in Shenzhen that aligned with the random walk model. In the second, the affective relationship between random walk and weak markets was considered. Lan et al. (2005) summarize the random walk model by referring to former scholars, to reveal a weak efficiency in the manner that continuous auction markets relate to "random walk" processes. By mining sign patterns and time sequences from China’s historical stock market information, it can be seen that China’s stock market has not yet reached weak efficiency.
Zhang and Zhang (2005) considered the trading price of futures as a research object, by using both the unit root test and the auto-correlation test. Concurrently they employed the ratio variance test with a multiple variance ratio test to empirically research the random walk hypothesis. Their results showed that the logarithms of major futures markets can not yet reject the hypotheses of the weak-form efficient market. Dai et al. (2005) while using the unit root method to verify the Composite Index of the Shanghai stock market, displayed that a vast majority of Shanghai stock market composite indices have a weak effect.
Regarding research into continuous auction simulation strategies, scholars have made great progress. Gode and Sunder (1993) first proposed a double-zero trading strategy: Zero-intelligence (ZI), ZI Unconstrained (ZI-U) and ZI with Constraint (ZI-C). The main difference between these strategies is the bidding interval: ZI-U rests on the premise that bidders give no consideration to resources, requiring random auction (loss) within the scope of market mechanisms; ZI-C rests on the premise that bidders fully consider their resources, requiring an auction where they suffer no loss. Duffy and Unver (2006) look to Gode and Sunder’s research to verify ZI when resources are limited and use a near zero auction model to explain the emergence of market bubbles-thus claiming the ability to predict market bubbles. Othman (2008) built a ZI agent model based on market forecasts where, under the premise that people are rational and desire to maximize profit, multiple transaction prices in the ZI model compliments the theory that rational participants help predict the price of the market. Based on the ZI strategy, Cliff and Bruten (1997) elicit the "Enhanced Zero" bidding strategy (ZIP, Zero-Intelligence Plus) based on information from historical markets and the ability to forecast prices. Here, the main idea is that buyers and sellers can continuously adjust profit margins in accord with historical transactions, to determine a new bid. Based on the ZI and ZIP policy, in view of the belief function, Gjerstad and Dickhaut (1998) put forward a model to calculate a maximum expectation which can adjust bids by relying on historical information to build self-confidence formulas and calculate a maximum expected profit. Finally, specific applications in this field include: The transaction model and the adaptive capacity auction model (Dawid, 1996; Preist, 1999), among others.
Xiaobo et al .(2006) proposed a strategy learning model based on the Particle Swarm Optimization (PSO) for individual learning behaviors in reference to cost and closed bilateral. By using the PSO algorithm to first summarize group and individual learning pathways and then to imitate learning in order to achieve a theoretical balanced level of bidding-they sought to rectify the one-on-one bargaining system of bidding laws. Next, Pengyu and Yijun (2006) proposed the hybrid theory for dynamic bidding. Xiaoyong and Qing (2008) sought to tackle the market-clearing mechanism to maximize combinatorial auctions by employing double auction transactions based on the shadow price. Wenjie and Jie (2008) then proposed a trading strategy based on the Markov chain and in turn verified how algorithms designed for ZI-C work alongside Markov tendencies. In situations where transaction prices for ZI-C continuous auction markets are coupled (based on the ZIP strategy), Shengfeng and Chengjian (2009) present the ZIP2 strategy, to achieve greater network efficiencies for resource allocation. Xu and Chengjian (2010) proposed a revised Risk-Based strategy from continuous double auctions and took advantage of the PSO to increase convergence of the double auction market price.
In summary, even though scholars have done much to test methods for weak continuous auction markets and the strategies for continuous auction simulations, still research is lacking to consider the relationship between and the manner in which simulation results guide continuous auction market participants. Presently, strategies for continuous auctions focus more upon historical data and transactional data. Likewise research pertaining to the best price in the relevant group is rare. By investigating the best price data and setting individual income maximization as a guideline, this paper aims at: (1) Putting forward a continuous bidding strategy (EOB strategy) based on the best price in the group; (2) Achieving near or greater than market equilibrium results for individual gain. The results of this research seek to provide a valuable theoretical basis and a feasible solution for those continuous double auction, random walking, market participants.
RANDOM WALKING TEST OF ZI-C TRANSACTION PRICE
Continuous auction market trading rules and the ZI-C strategy: There are M buyers and N sellers in the continuous auction market and the market environment of M:N represents a symmetrical relationship. In order to facilitate this study a simplified market provides that: (1) Each buyer can only buy a commodity, each seller can only sell a commodity and the goods held by buyers and sellers are homogeneous; (2) Each buyer holds a different valuations of goods, noted by: V1, V2,…, Vm; (3) The costs to each seller, noted by: C1, C2,…, Cm, differ from the estimates of buyers and sellers and also differ from costs shown on the supply and demand curves in the continuous auction market.
ZI-C bidding strategy is a scenario where the buyer’s bid is a random number occurring between the minimum price and the buyer’s valuation while the seller’s quotation is a random number uniformly distributed between the seller’s cost and the price ceiling (Gode and Sunder). Assuming the minimum price in the continuous auction market is 0, the price-cap is 100, so, a mathematical representation for the ZI-C bidding strategy is: Bi-U(0, Vi), where Vi is the value of resources obtained by the “i” buyer. The formula for a ZI-C selling bid is:
Aj-U(Cj, 100) |
where, “C” is the cost for the “j” seller.
Based on Gode and Sunder, this study uses the continuous auction market trading rules. Specifically: (Rule 1) a buyer “i”, may bid “Bi” according to their own valuation “Vi” of goods - while a seller “j”, auctions “Aj” according to their individual cost “Cj”, under the rules: BI≤Vi, Aj≥Cj. (Rule 2) At any time “t”, randomly selected by a buyer or seller, the buyer bidding “Bi” marks the highest bid “B-best” while the seller auctions “Aj” and marks the lowest bid as “A-best”. (Rule 3) At the time B-best≤A-best, the corresponding bidding party completes the transaction and the price equals half of both auctions’ sum (i.e., TP(i, j) = 1(B-best+S-best)). Following the first transaction, the second highest bid of the buyer becomes “B-best” while at the same time, the second lowest bid by the seller becomes “A-best”. This process continues until all bids are taken and finally, the bidding ceases with both parties leaving the market. (Rule 4) No dealing party re-issues the bid, at the time of “t+1”, repeat rule 2 and rule 3. (Rule 5) Repeat the above rules 1-4 as long as all Bi < Aj holds true. End.
Random walking test of transaction price sequence: According to previous studies, the Runs test and DF testing are the two most preferred methods for testing transaction price in the ZI-C strategy.
| Table 1: | Random walking test results of ZI-C transaction price sequence |
 | |
The Runs Test ideological states: Let “N” be the total number of samples in a price sequence {TPt} with ni (i = 1, 2, 3) to represent the number of price changes in various directions, where “n1” is the number for positive price changes, “n2” is the number for negative price changes, “n3” is the number for events with no price change and “M” is the actual number of runs. So, the {TPt} sequence expected number of runs is:
with a variance of:
From the standardized normal variable:
where, M>E(m), uses an adjustment coefficient of 0.5 and when M<E(m) the 0.5 adjustment coefficient should be subtracted. When “N” is sufficiently large, then “K” is close to zero and the variance is 1.0 in a normal distribution. Accordingly, at the 1% significance level, the critical value of “K” is 2.33, if the value of “K” lies within the range (-2.33, 2.33), then we accept the assumption of randomness for the stock price. Otherwise, we conclude that stock price is moving with a trend.
The DF testing method was created by Dickey and Fuller on the premise that it has: a first-order autoregressive process for price sequencing:
where εt is independent and evenly distributed and where E(εt) = , D(εt) = E(εt2) = σ2<∞. Parameters ρ can be tested, so that if ρ = 1, the price sequence {TPt} follows a random walk process. If ρ<1, then the price sequence obeys the stable first-order autoregressive process and the least squares estimation of the parameters is:
The estimated value of the standard deviation for ![]() is
is ![]() :
:
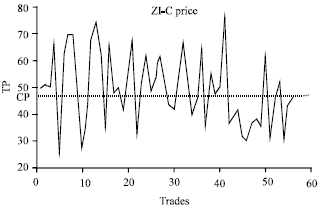 | |
| Fig. 1: | ZI-C Strategy Transaction Price |
The tT statistic for ρ is ![]() . Further, ρ = 1 can use
. Further, ρ = 1 can use ![]() in addition with tT to conduct tests while the critical value of
in addition with tT to conduct tests while the critical value of ![]() and tT (Enders et al., 2012) at a 1% confidence interval issues the critical value -13.7 for
and tT (Enders et al., 2012) at a 1% confidence interval issues the critical value -13.7 for ![]() and -2.58 as a critical value for tT.
and -2.58 as a critical value for tT.
We selected 100 ZI-C strategies from the buyer and seller to perform a "random walk" experiment of transaction prices in a ZI-C simulation. Conducting the test, adhering to the market rules stated above, we discovered that after 30 simulations, each result was remarkably similar with randomly selected transaction price data. Figure 1 shows the ZI-C Transaction Price Strategy. “CP” in Fig. 1 corresponds to a balanced equilibrium price that was achieved by the market.
Conducting a Runs test and DF test for the ZI-C Transaction Price Sequence produced the results are shown in Table 1.
Test results revealed that: below the 1% confidence level, the transaction price of the ZI-C strategy passed the Runs test and the DF test. This proves that the transaction price of the ZI-C strategy is in line with the "random walk" model in the continuous auction market.
EYE-ON-BEST STRATEGY
The main idea of continuous bidding strategy (EOB) based on the best group best price (Eye-On-Best) focuses on the buyer’s highest bid and the seller’s minimum bid in the market (i.e., buyers and sellers each auction). In accord with both sides’ bids it revises a new bidding strategy, in order to elicit higher individual incomes. Specifically: assume that at the time “t” in a continuous auction market, the highest bid of the buyer is “B-best(t)” while the seller’s minimum bid is “A-best(t)”. At the time of “t+1”, buyers and sellers bid in accordance with the best price “B-best(t)” and “A-best(t)” at the time of “t” and concurrently determine their new bids whether the seller and the buyer close the deal at the time “t” or not. If at time “t”, buyers and sellers can trade in the market, indicating that buying and selling is profitable, the offers can continue according to the current prices at time “t+1”. This is all taken into consideration with factors such as: increasing revenue, the buyer reducing a minimum on the basis of B-best(t); and the seller increasing a minimum based on A-best(t). If at time “t” buyers and sellers cannot trade, indicating that buyers or sellers will not make a profit, the offer should be adjusted to reissue the at the time “t+1”. In regard to fixing profit, the buyer may adjust minimal value on the basis of B-best(t) while the seller adjusts on the basis of A-best(t) to mutually achieve a beneficial transaction.
In a scenario where the buyer bids at time t+1 and makes an adjustment to the bid based upon B-best(t), at time t the adjustment only yields a minimum Δ; while at the same time the seller at time t+1 makes an adjustment to the bid based upon A-best(t), at the time t, the adjustment only yields a minimum Δ. Meanwhile while constrained by bounded rationality the buyer can not bid higher than their disposable resources allow (Bi≤Vi) and the seller can not bid less than the cost (Aj≥Cj). Based upon these assumptions we derive the mathematical expression for an EOB strategy auction, at the moment t+1:
The buyer bidding strategy for i is:
| (1) |
The seller’s bidding strategy for i is:
| (2) |
From Eq. 1 and 2 above, buyers and sellers adjust bids according to the EOB strategy at the time t+1. If buyers and sellers agree to a transaction at time t, then at the time t+1, the buyer should lower the bid while the seller should raise the bid, so that, B-best(t)-Δ decreases the value in the buyer’s bidding formula and A-best(t)+Δ increases the value in the seller’s bidding formula. If buyers and sellers do not achieve a trade at time t, then at the time t+1, the bid should be raised for the buyer and reduced for the seller: thus the value of B-best(t)+Δ increases the value in the buyer’s bidding formula and the value of A-best(t)-Δ decreases the value in the seller’s bidding formula.
EXPERIMENTAL DESIGN
In our experiment 100 buyers and 100 sellers were used for a test market where each buyer or seller could trade one item under the position substitution principle. To achieve a random market, as we expect exists in (ZI-C) strategy and which is required for an EOB policy, each supply and demand curve was reproduced 10,000 times to minimize any uncertainty resulting from random factors to the experiment. Thus, the following individual incomes represent the average of 10,000 experiments.
We used individual gain level as the variable to measure the various impacts that bidding strategies had upon revenue. Buyer’s individual gain equals resources owned minus the transaction price. Seller’s individual gain equals the transaction price minus its cost. The mathematical expressions for individual gains are:
| (3) |
| (4) |
In Eq. 3 and 4 above, profit-buye(i)r is the buyer’s individual gain from the i position, Vi is the resources owned by the buyer at the i position and TP(i, j) is the transaction price when buyer in the i position and seller in the j position reach a trade. Here, “i" = 1, 2,...m and j = 1, 2,...n. The profit-buye(j) is the seller’s Individual gain from the j position and Cj is the seller’s costs at the j position.
Meanwhile, based on profit maximization theory, we established a standard to measure the merits for each policy and judged whether it could achieve an equalized individual gain or not. If individual gains were close to equilibrium, the individual could profit; if individual gains were greater than the equilibrium, there was excessive profit. We expected that the individual gain produced by the strategy would not be less than a balanced individual gain, meaning that individuals are able to reap excessive profit. Individual equalized gain equals the buyer’s individual gain and the seller’s individual gain at market equilibrium, where the former equals the resources occupied by the buyer minus the market equilibrium price, the latter equals the market equilibrium price minus the cost to the seller. The specific mathematical formula follows:
| (5) |
| (6) |
The CP from formula 5 and 6 above is the theoretical transaction price in market equilibrium, Competitive-buyer(i). For the buyer this is individual gain at the i position in market equilibrium (i = 1, 2þ,m) while Competitive-seller(j) is for the seller individual gain at the j position in market equilibrium (i = 1, 2þ,n) and CP is the price in market equilibrium.
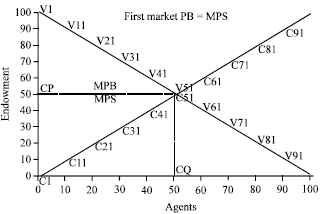 | |
| Fig. 2: | First supply and demand curve |
In order to avoid influences resultant from bidding strategies by traders in a continuous auction market, the present study uses a position substitution method. The position substitution assumes that bidding strategy is fixed at all positions in the market (in addition to the test position). If the test position changes with a different bidding strategy then bidding strategy in other positions remains fixed. Specific experimental procedures follow where we assume that all policies available in the market are ZI-C, respectively, statistics for individual gains in the ZI-C strategy at the position of Vi (i = 1, 11,...,91) and Cj (j = 1, 11,...,91). Afterward, one follows the other in the EOB strategy to replace Vi (i = 1, 11,..., 91) and Cj (j = 1, 11,..., 91) so that successive individuals record profits in the EOB strategy in the test position. And then when comparing levels of gain in the same position of the ZI-C strategy and EOB strategy, one should finally compare individual gains in the same position under market equilibrium.
Note: Strategy may be affected by a shift in supply and/or demand. Therefore in order to verify that EOB strategies are more capable than ZI-C strategies in scenarios where supply and demand curves shift, we divided the market into the following three categories according to buyer and seller abilities to control the market (we divided the buyer’s market power MPB and the seller’s market power MPS). First, a bilateral market: where buyers and sellers share the same market resources, MPB = MPS; Second, a buyer’s market where a buyer has superior market resources, MPB>MPS and Third, a seller’s market where a seller has superior market resources, MPB<MPS. Equation follow:
| (7) |
| (8) |
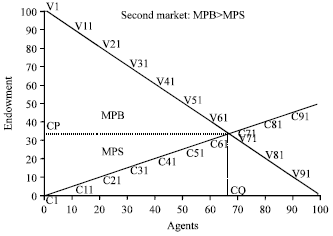 | |
| Fig. 3: | Second supply and demand curve |
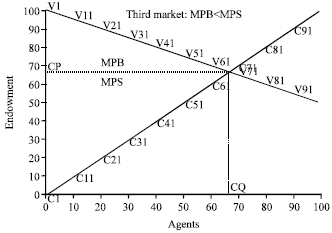 | |
| Fig. 4: | The third supply and demand curve |
Above in Eq. 7 and 8, CK is the buyer’s or seller’s corresponding position from the supply and demand curves in market equilibrium. Three types of supply and demand curves correspond to the following Fig. 2-4.
These three supply and demand curves were selected in respective Runs tests and DF tests. The test results are shown below in Table 2 of the ZI-C strategy transaction price sequence random walk under the curves.
Test results revealed that below a 1% confidence level, the transaction price of the ZI-C strategy passes the runs test and DF test in all three curve types. This shows that in the three categories under the curve selected, the transaction price of the ZI-C strategy continues to comply with the random walk model.
EXPERIMENTAL RESULTS AND ANALYSIS
MATLAB’S ability compute and map out simulations, makes it a tool increasingly used by a majority of scholars for continuous auction market research. Likewise, this study used Matlab 2011 to perform tests. Supply and demand curves were selected according to the market resources of buyers and sellers in the market; which in turn was divided into three categories. Analysis of these experimental results follows.
In a bilateral market, buyers and sellers share equal market resources (MPB = MPS). The market structure is shown in Fig. 2 and the simulation data is shown in Table 3.
Table 3 shows that, buyers and sellers can achieve greater individual returns by using the EOB strategy when they share equal market resources. In this scenario, individual returns from the EOB strategy are higher than the individual returns from the ZI-C strategy. Further, the EOB strategy can yield higher returns in this environment. In a buyer’s market (MPB>MPS) the buyer has a majority share of market resources. This market structure is shown in Fig. 3 and the simulation data for this structure is shown in Table 4.
Table 4 shows that, in the case where the buyer has superior market resources, the EOB strategy can achieve greater individual returns than the ZI-C strategy for the buyer in dominant position, but it will not reach market equilibrium. The EOB strategy can achieve both greater individual returns than the ZI-C strategy for the seller of inferior position and more income than a balanced revenue scenario. Above all, it shows that where resources are unequal, this strategy is more conducive to achieve excess returns.
In a seller’s market (MPB<MPS), the seller holds a greater share of market resources. The market structure is shown in Fig. 4 while the simulation data is shown in Table 5.
Table 5 shows that, in the case where a seller holds more market resources, the performance runs contrary to when the buyer has a superior position, with the same benefit now on the side of the sellers.
When comparing Individual earnings from the EOB strategy and the ZI-C strategy in differing market conditions, the following conclusions can be drawn: if buyers and sellers share equal market resources or whether the buyer or the seller holds superior resources, then the EOB strategy can achieve about 15-23% greater personal returns than the ZI-C strategy.
In different markets, comparing individual returns from the EOB strategy, with the ZI-C strategy and individual balanced income, the following conclusions can be drawn: first, the person in an inferior resource position can achieve individual returns from the ZI-C strategy to reach approximately 95% of balanced individual gain.
| Table 2: | Random walking test results of ZI-C Transaction price sequence in three market power |
 | |
| Table 3: | Result of first market MPB = MPS |
 | |
| Table 4: | Result of second market MPB>MPS |
 | |
| Table 5: | Result of third market MPB<MPS |
 | |
However, the maximum individual return of the EOB strategy can achieve more than a balanced individual gain. Second, the resource dominant party can achieve individual returns from the ZI-C strategy to up to 87% of the individual balanced gain. Finally, the individual income of the EOB strategy can reach up to 97% of the individual equalized return. In these scenarios the individual returns from the EOB strategy are still higher than the individual income from the ZI-C strategy.
The random walking ZI-C strategy was verified by transaction prices. A weak efficient market environment can be simulated using the ZI-C strategy. On this basis, using group optimal pricing information in the market, a group optimal bidding strategy (EOB) can be designed to improve individual returns in continuous auction markets. The experimental results show that: in continuous auction markets: (1) The EOB strategy is significantly better than the ZI-C strategy to achieve individual returns greater than the ZI-C strategy in various market environments; (2) An EOB strategy can help the individual in an inferior resource position because the EOB strategy is best suited for bidding when in an inferior position; and (3) in a continuous auction market, the random walk EOB strategy reveals that group competitive bidding is a decisive factor.
Therefore, in a continuous auction market, individual returns can be improved by using all known information to design a bidding strategy. The resource inferior position can improve individual returns by using the EOB strategy. On this basis, first of all, bidding strategies can be used to achieve greater returns in a variety of market positions. This provides both a theoretical basis and feasible ideas for intelligent algorithm-assisted bidding practitioners. Secondly, this method offers a new tool for use in computer aided financial market simulations.