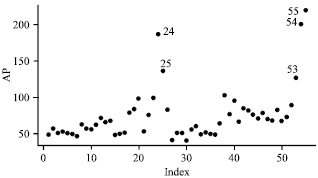
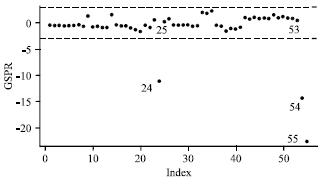
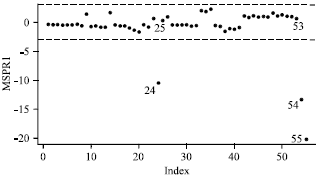
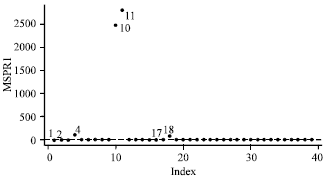
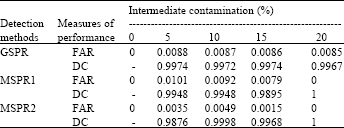
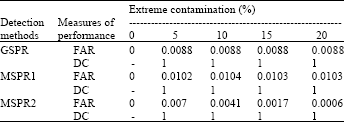
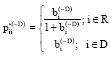Research Article
Modified Standardized Pearson Residual for the Identification of Outliers in Logistic Regression Model
Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Syaiba Balqish Ariffin
Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia