Research Article
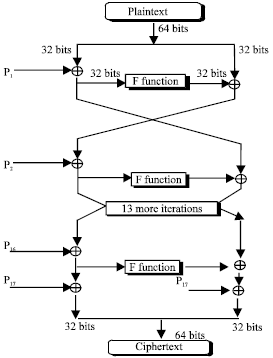
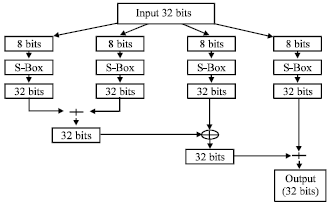
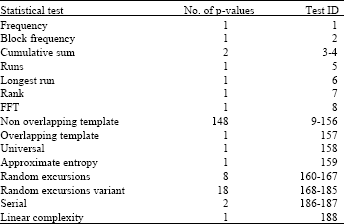
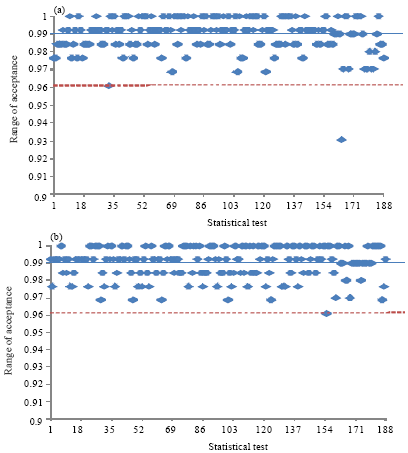
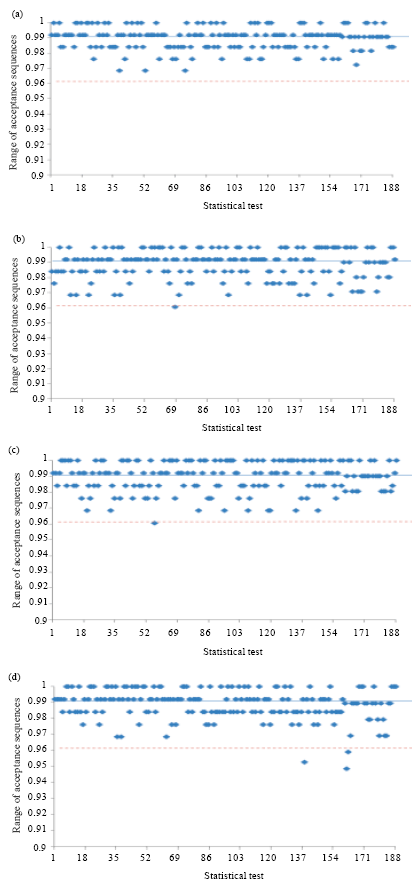
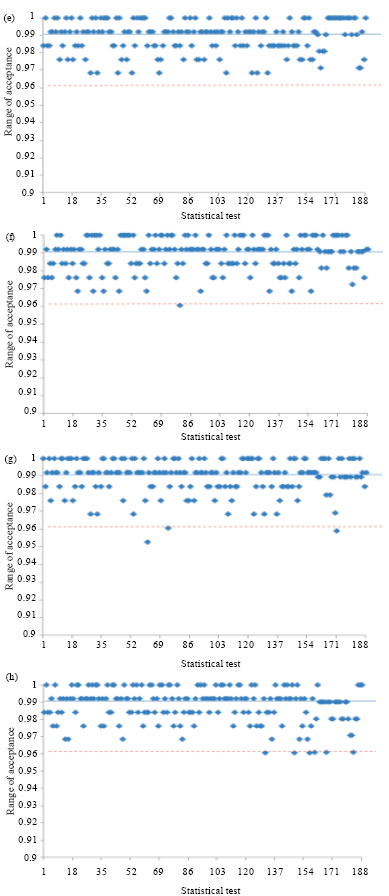
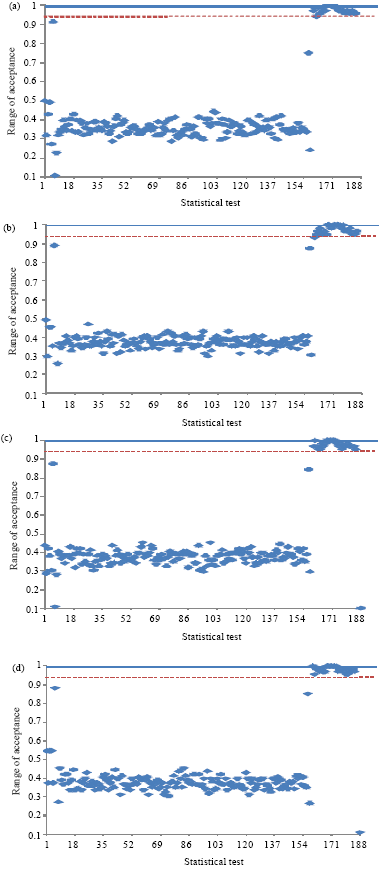
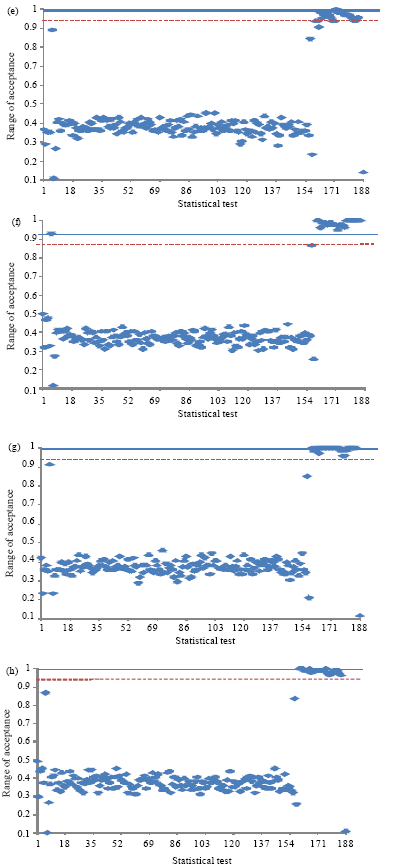
Randomness Analysis on Blowfish Block Cipher Using ECB and CBC Modes
Department of Information Technology, University Utara Malaysia, 06010, Sintok, Malaysia
Ramlan Mahmood
Faculty of Computer Science and Information Technology, University Putra Malaysia, Erdang, Selangor, Malaysia
Faudziah Ahmad
Department of Information Technology, University Utara Malaysia, 06010, Sintok, Malaysia
Mohammed S. Mechee
Department of Mathematics, Faculty of Mathematics and Computer Sciences, Kufa University, Najaf, Iraq