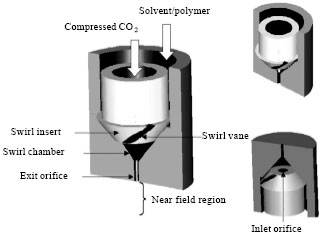
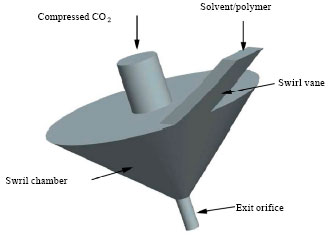
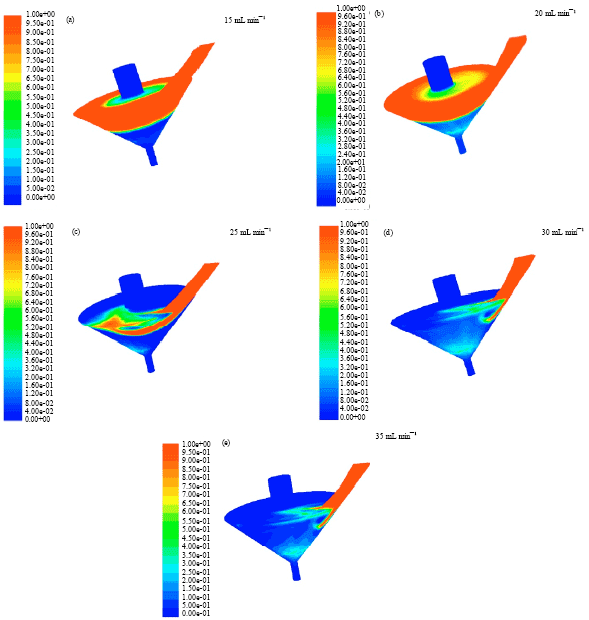
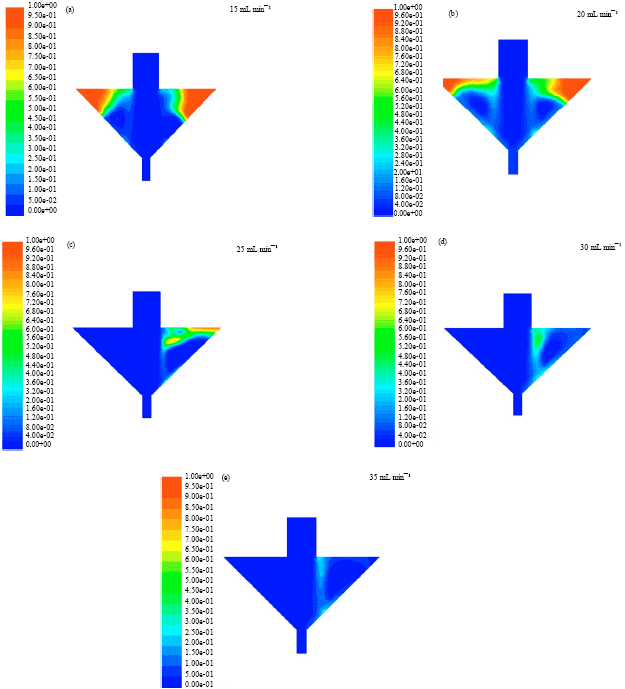
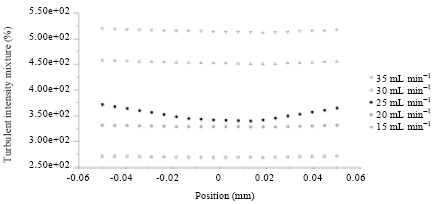
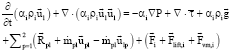Research Article
CFD Simulation of the Flow in Jet-swirl Nozzle for Preparing Nano-drug During a SEDS Process
Laboratory of Bio-pharmacy of Agricultural, College of Chemistry and Pharmaceutical Science, Qingdao Agricultural University, Qingdao, 266109, China
Zhihui Hao
Laboratory of Bio-pharmacy of Agricultural, College of Chemistry and Pharmaceutical Science, Qingdao Agricultural University, Qingdao, 266109, China
Dedong Hu
The College of Electromechanical Engineering, Qingdao University of Science and Technology, Qingdao, 266061, China
Leilei Wang
Laboratory of Bio-pharmacy of Agricultural, College of Chemistry and Pharmaceutical Science, Qingdao Agricultural University, Qingdao, 266109, China