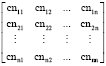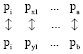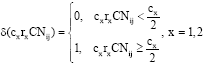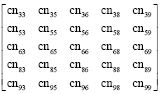Research Article
An Optimization Model for the Interconnection among Peers of the P2P Network
Tangshan Key Laboratory of Informationization Technologies and Engineering Control, School of Management, Hebei United University, China
Tian Xiaoyu
Tangshan Key Laboratory of Informationization Technologies and Engineering Control, School of Management, Hebei United University, China
Tang Zhongbin
Department of Fundamental Courses, Xuzhou Air Force College, China