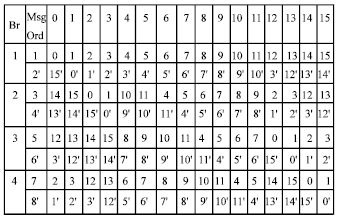
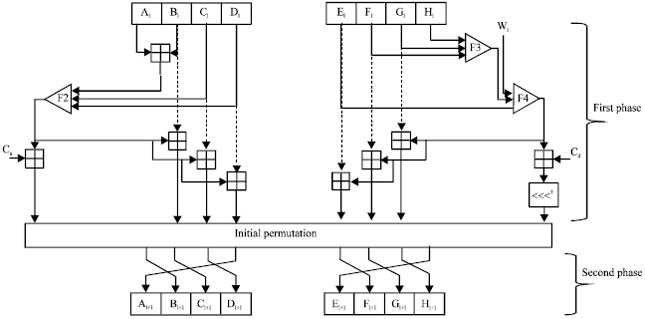
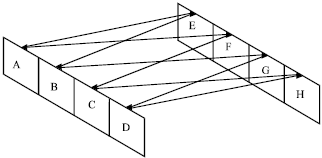
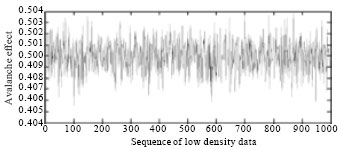
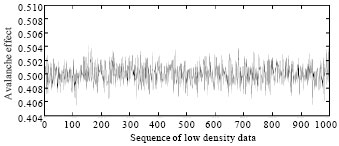
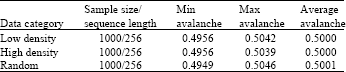
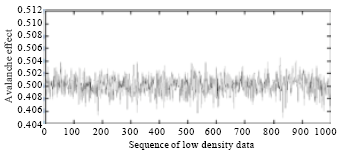
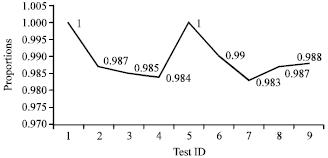
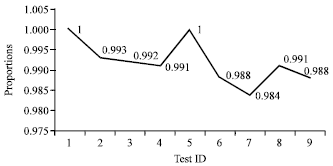
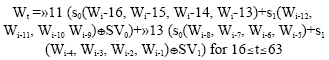Research Article
Diffusion and Statistical Analysis of STITCH-256
College of Information and Technology, Universiti of Tenaga Nasional, KM7, Jalan IKRAM-UNITEN, Serdang, 43600 Selangor, Malaysia
R. Mahmod
Faculty of Computer Science and Information Technology, Universiti Putra Malaysia, 43600 Seri Kembangan, Selangor, Malaysia
M.R. Z`aba
Cryptography Lab., MIMOS Berhad, Technology Park Malaysia, 57000 Bukit Jalil, Kuala Lumpur, Malaysia
N.I. Udzir
Faculty of Computer Science and Information Technology, Universiti Putra Malaysia, 43600 Seri Kembangan, Selangor, Malaysia
Z.A. Zukarnain
Faculty of Computer Science and Information Technology, Universiti Putra Malaysia, 43600 Seri Kembangan, Selangor, Malaysia