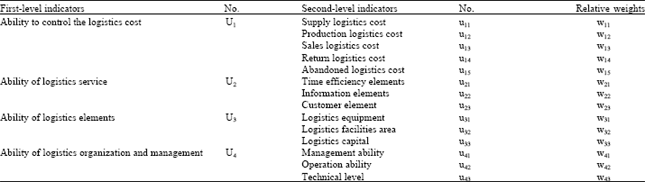
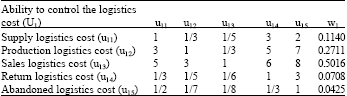
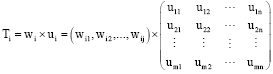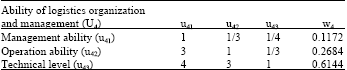Research Article
Study on Logistics Capability of Manufacturing Enterprise via AHP and Fuzzy Evaluation
School of Economics and Management, Hubei Polytechnic University, Huangshi, 435003, China
Shujie Yun
Department of Basic, Henan Mechanical and Electrical Engineering College, Xinxiang, 453000, China
Xiaorong Huang
School of Economics and Management, Hubei Polytechnic University, Huangshi, 435003, China
Jingyuan Xing
School of Economics and Management, Hubei Polytechnic University, Huangshi, 435003, China
Yazhou Xiong
School of Economics and Management, Hubei Polytechnic University, Huangshi, 435003, China