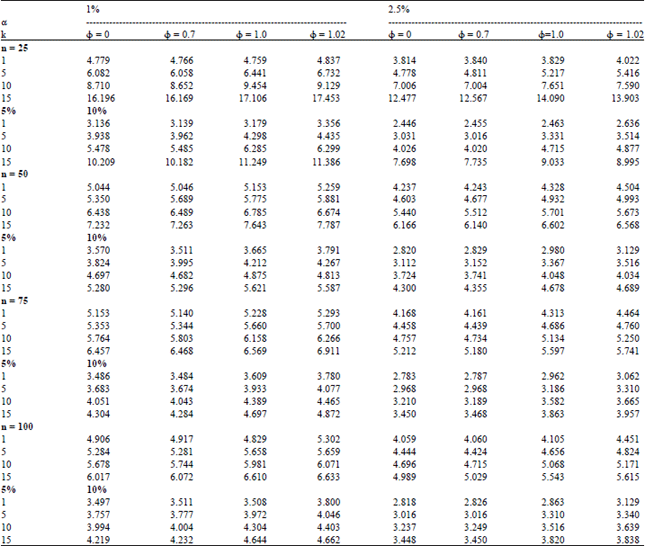
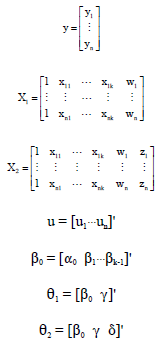Research Article
Likelihood Ratio Type Test and its Critical Values for Structural Change of Unknown Changepoint
Department of Quantitative Analysis, College of Business Administration, King Saud University, Riyadh 11451, Kingdom of Saudi Arabia
Mahbuba Yeasmin
EKRA Institute, Melbourne, Victoria 3166, Australia
Gazi Mahabubul Alam
Academic Performance Enhancement Unit, University of Malaya, 50603 Kuala Lumpur, Malaysia