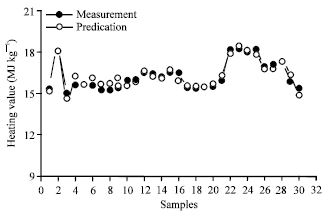
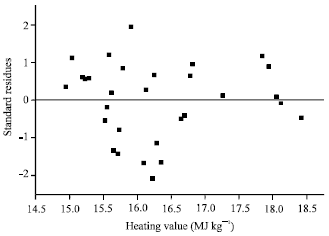
Research Article
Prediction of Heating Values of Oil Palm Fronds from Ultimate Analysis
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, 31750 Tronoh, Perak, Malaysia
Shaharin Anwar
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, 31750 Tronoh, Perak, Malaysia
Bambang Ariwahjoedi
Department of Fundamental and Applied Science, Universiti Teknologi PETRONAS, 31750 Tronoh, Perak, Malaysia