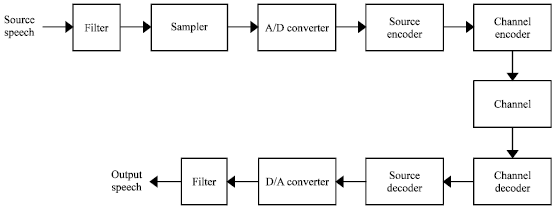
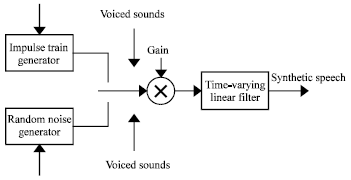
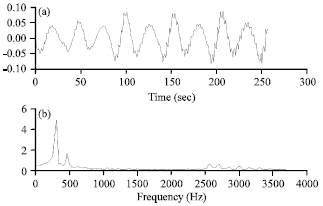
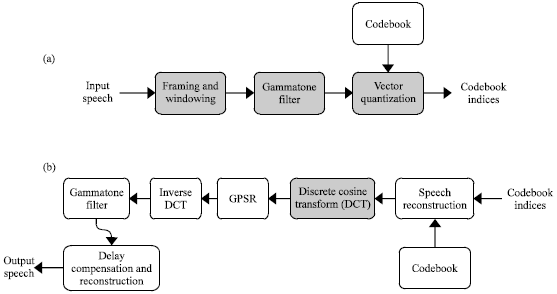
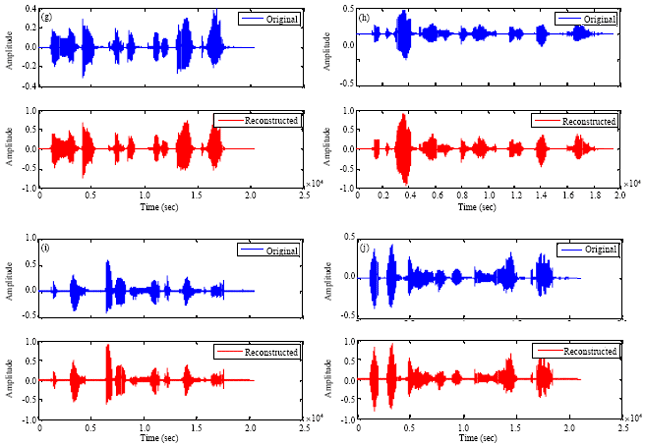
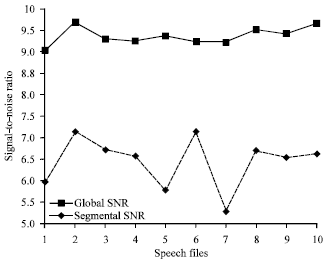
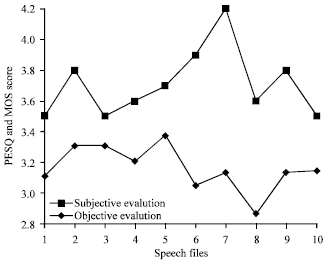
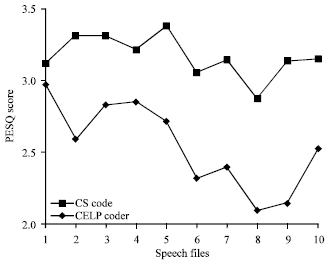
Research Article
Development of Low Bit Rate Speech Encoder based on Vector Quantization and Compressive Sensing
Department of Electrical and Computer Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
T.S. Gunawan
Department of Electrical and Computer Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
O.O. Khalifa
Department of Electrical and Computer Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
M. Kartiwi
Department of Information System, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
A. Sulong
Department of Electrical and Computer Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
K. Abdullah
Department of Electrical and Computer Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia
N.F. Hasbullah
Department of Electrical and Computer Engineering, International Islamic University Malaysia, Jalan Gombak, 53100 Kuala Lumpur, Malaysia