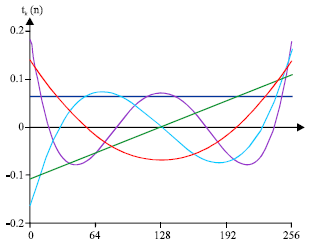
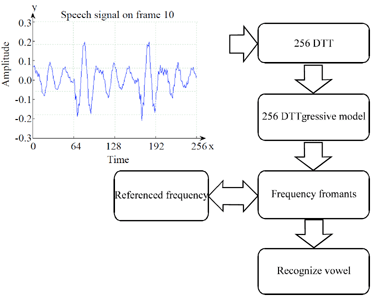
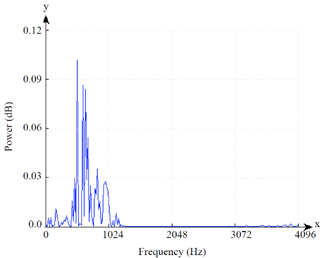
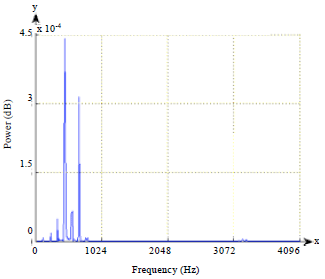
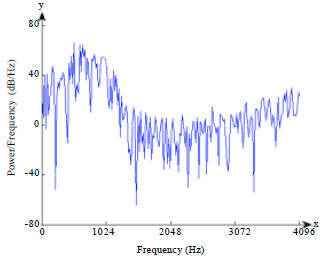
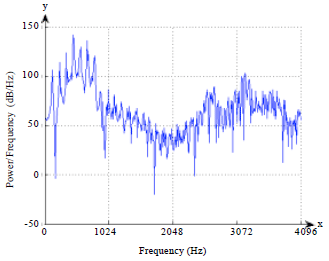
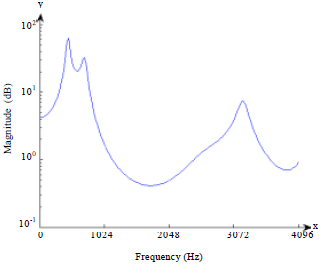
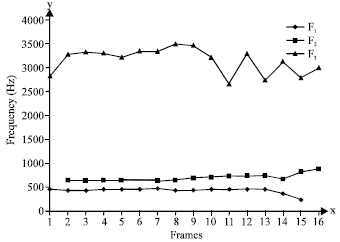
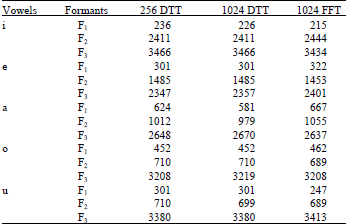
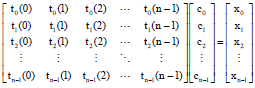Research Article
Vowel Recognition using Discrete Tchebichef Transform
Faculty of Information and Communication Technology, Universitas Dian Nuswantoro Imam Bonjol No. 206, Semarang 50131, Indonesia
Nur Azman Abu
Faculty of Information and Communication Technology, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, Melaka, 76100, Malaysia
Nanna Suryana
Faculty of Information and Communication Technology, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, Melaka, 76100, Malaysia