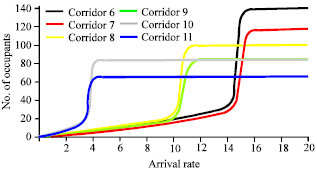
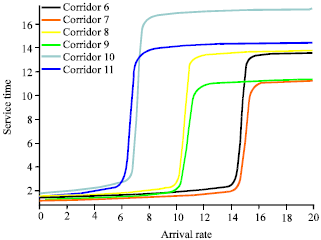
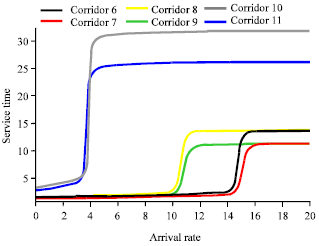
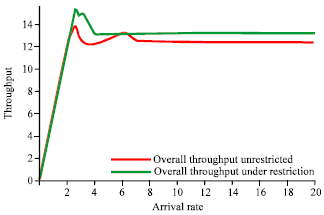
Research Article
Pedestrian Performance Measures of an M/G/C/C State Dependent Queuing Network in Emergency
School of Distance Education, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
N.A. Ghani
School of Distance Education, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
A.A. Kamil
School of Distance Education, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
A. Mustafa
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
L.A. Kawsar
School of Distance Education, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
N.A. Ghani
School of Distance Education, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
A.A. Kamil
School of Distance Education, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
A. Mustafa
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia