Research Article
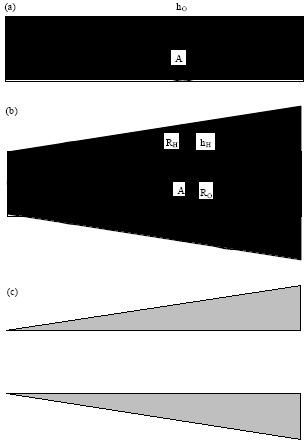
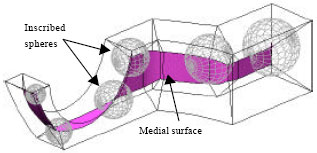
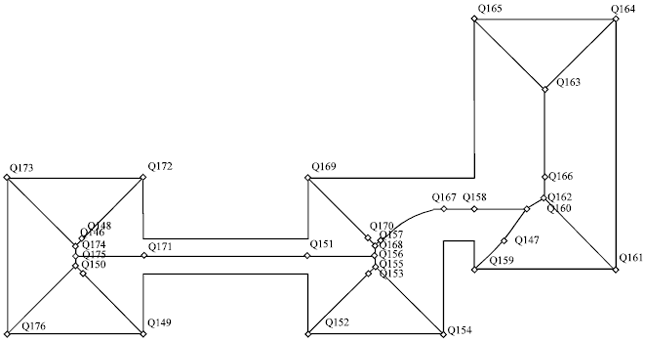
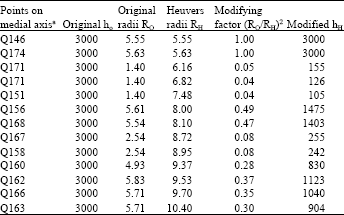
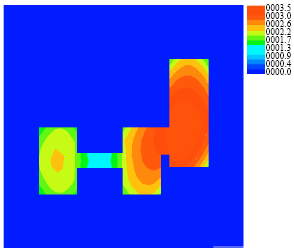
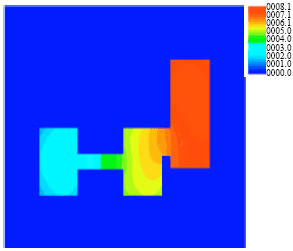
Optimization of Insulation Padding for Directional Solidification
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Xiaohui Chen
Department of Civil and Structural Engineering, Kroto Research Institute, Sheffield University, S3 7HQ, United Kingdom
Lin Chao
Department of Materials, University of Oxford, Parks Road, Oxford, OX1 3PH, United Kingdom