Research Article
A Test for Testing the Equality of Two Covariance Matrices for High-dimensional Data
School of Applied Statistics, National Institute of Development Administration, Bangkapi District, Bangkok, 10240, Thailand
Samruam Chongcharoen
School of Applied Statistics, National Institute of Development Administration, Bangkapi District, Bangkok, 10240, Thailand









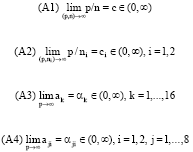
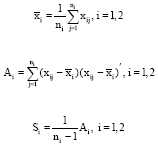
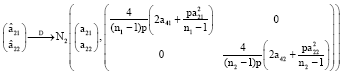
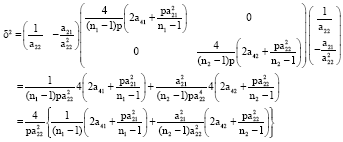
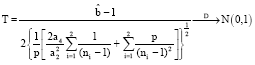
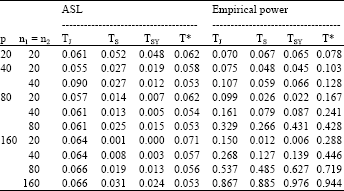


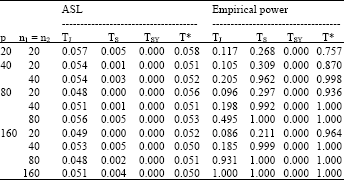
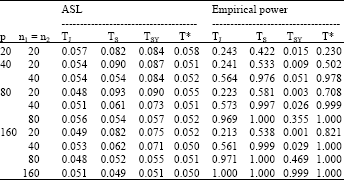
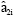 , i = 1,2.
, i = 1,2.