Research Article
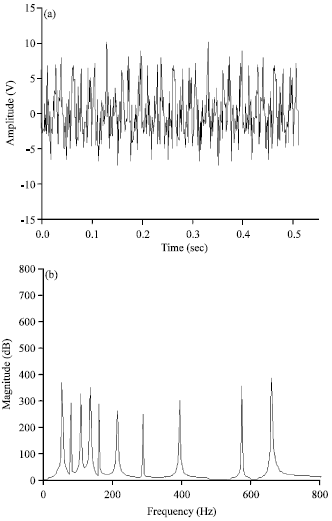
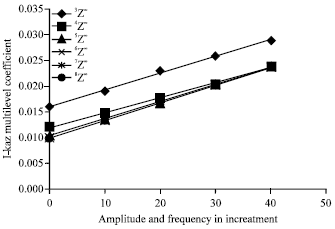
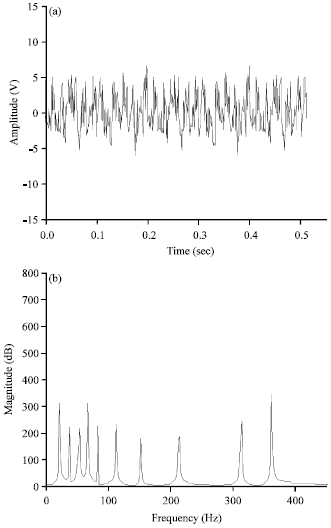
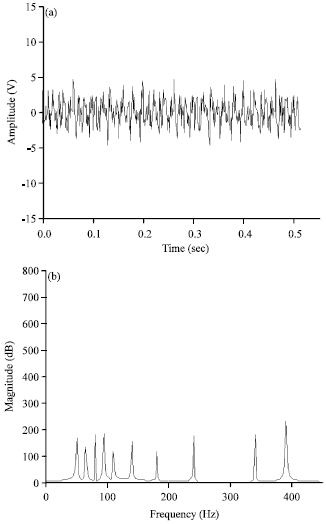
Integrated Kurtosis-Based Algorithm for Z-Notch Filter (I-kazTM) Multilevel Coefficients Responses toward the Simultaneous Changes in Amplitude and Frequency of Signals
Department of Mechanical and Manufacturing Engineering, Universiti Kuala Lumpur Malaysia France Institute, 43650 Bangi, Selangor, Malaysia
M.Z. Nuawi
Department of Mechanical and Materials Engineering, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia
A.Y. Md Said
Department of Mechanical and Manufacturing Engineering, Universiti Kuala Lumpur Malaysia France Institute, 43650 Bangi, Selangor, Malaysia
J.A. Ghani
Department of Mechanical and Materials Engineering, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia
S. Abdullah
Department of Mechanical and Materials Engineering, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia