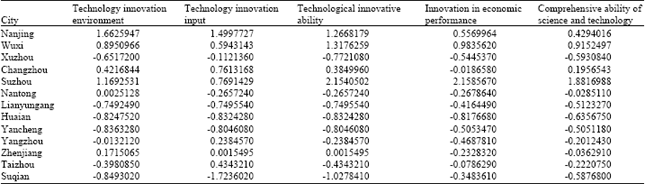
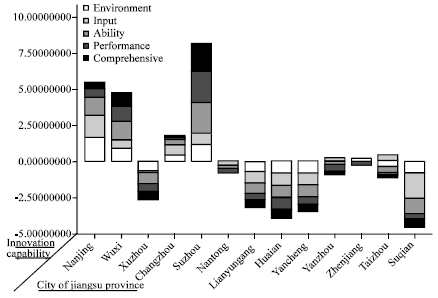
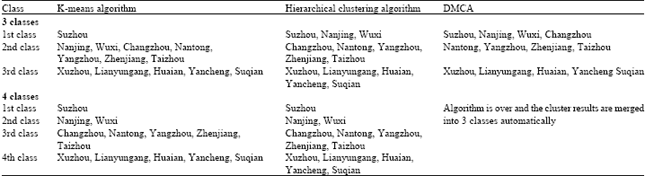
Research Article
Dynamic Merge Clustering Algorithm and its Application in Evaluation of the Regional Scientific and Technological Innovation Capability
School of Management, Xuzhou Institute of Technology, Jiangsu Xuzhou, China
Tian Xue-Mei
Faculty of Higher Education, Swinburne University of Technology, Melbourne, Australia