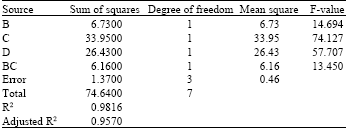
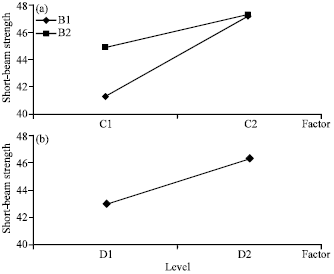
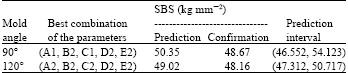
Research Article
Two-dimensional Stamp Forming Analysis for Thermoplastic Composites
Department of Industrial Engineering and Management, National Yunlin University of Science and Technology, Taiwan, Republic of China
Tao-Hsing Wang
Department of Industrial Engineering and Management, Asia-Pacific Institute of Creativity, Taiwan, Republic of China
Cheng-Tao Yu
Department of Industrial Engineering and Management, National Yunlin University of Science and Technology, Taiwan, Republic of China
Bor-Wen Cheng
Department of Industrial Engineering and Management, National Yunlin University of Science and Technology, Taiwan, Republic of China