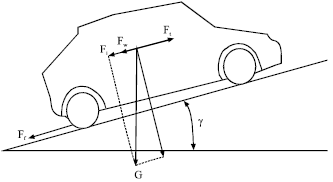
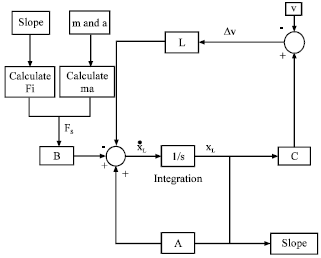
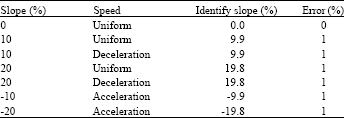
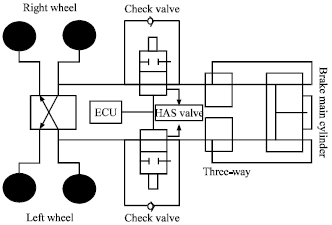
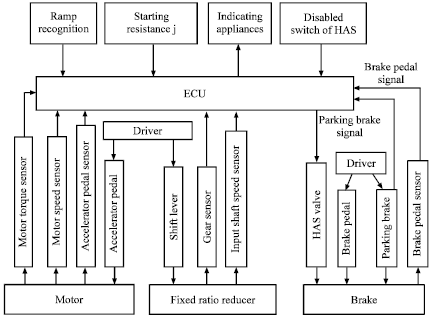
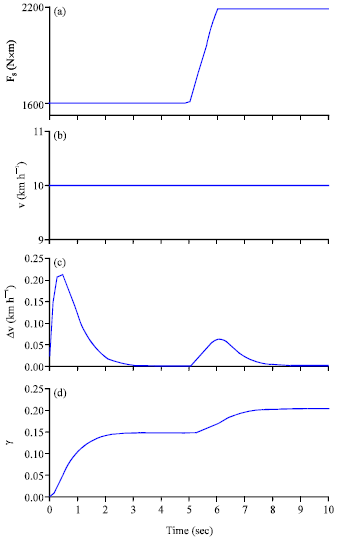
Research Article
Control Strategy for Hill Starting of Electric Vehicle
State Key Laboratory of Mechanical Transmission (SKLMT), Chongqing University, China
Chen Xi
State Key Laboratory of Mechanical Transmission (SKLMT), Chongqing University, China
Du Rui
State Key Laboratory of Mechanical Transmission (SKLMT), Chongqing University, China
Zhang Yi
Department of Mechanical Engineering, University of Michigan-dearborn, United State of America