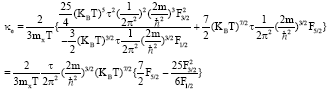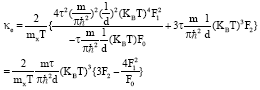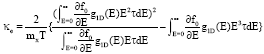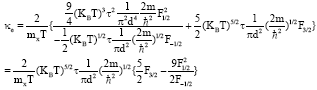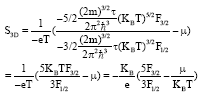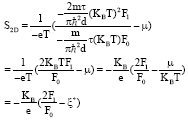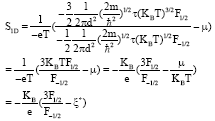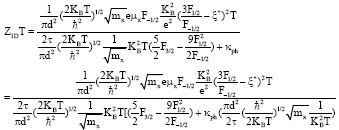Research Article
Investigation of Temperature Dependence Thermoelectric Figure of Merit (ZT) in Low-dimensional Bi2Te3
Islamic Azad University, Parsabad Moghan Branch, Parsabad, Iran
Hasan Hossein Zadeh
Department of Mathematics, Ardabil Branch, Islamic Azad University, Ardabil, Iran