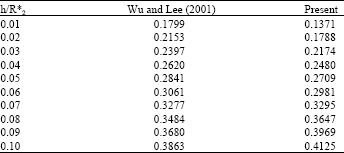
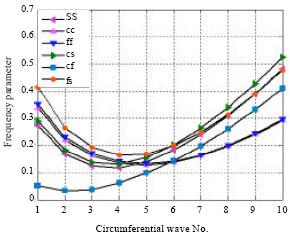
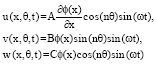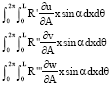Research Article
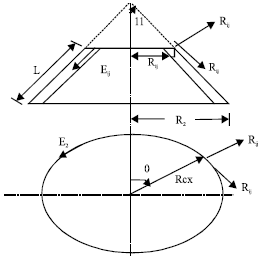
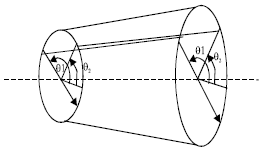
Free Vibration Analysis of Truncated Conical Composite Shells using the Galerkin Method
Department of Mechanical Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran
Reza Ansari
Department of Mechanical Engineering, University of Guilan, Rasht, Iran
Rahim Bakhoday Paskiaby
Department of Mechanical Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran