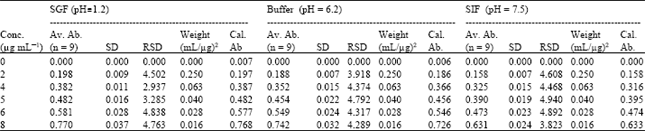
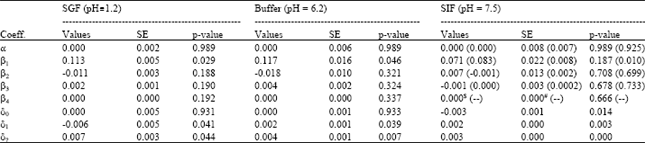
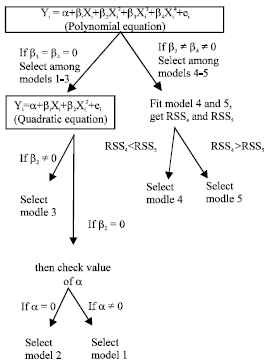
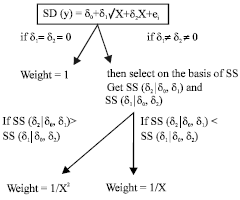
Research Article
Development of Analytical Method Using Classical Regression Technique
Department of Pharmaceutical Sciences and Drug Research, Punjabi University, Patiala 147 002, India
Harmeet Kaur
Department of Medicinal Chemistry, National Institute of Pharmaceutical Education and Research, Mohali, India
Sunil Gupta
Department of Pharmaceutical Sciences and Drug Research, Punjabi University, Patiala 147 002, India