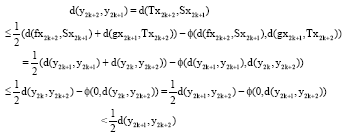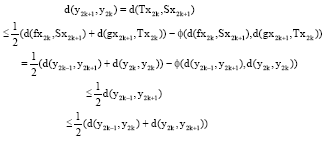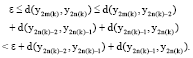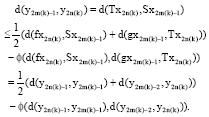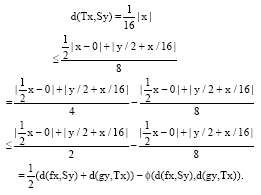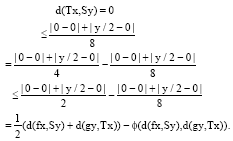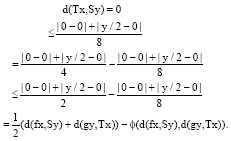Research Article
Some Common Fixed Point Theorems for Weakly Cf,g-contractive Mappings in Complete Metric Spaces
Department of Mathematics, Gilan-E-Gharb Branch, Islamic Azad University, Gilan-E-Gharb, Iran
H. Hosseinzadeh
Department of Mathematics, Ardebil Branch, Islamic Azad University, Ardebil, Iran