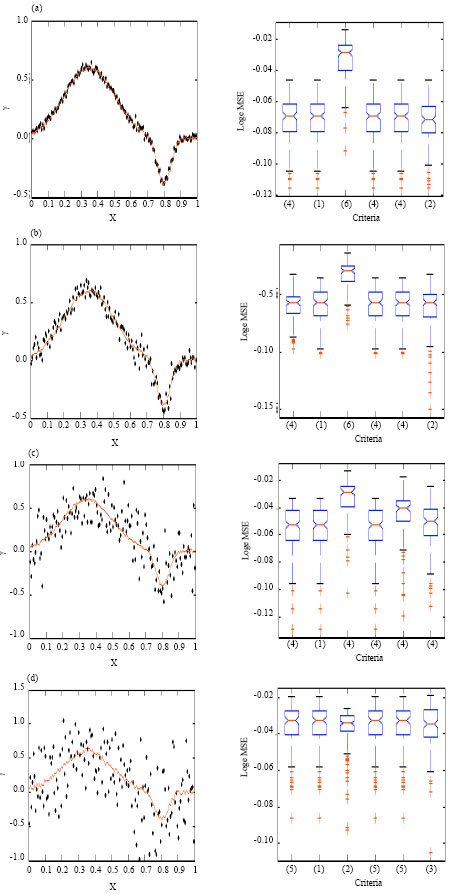
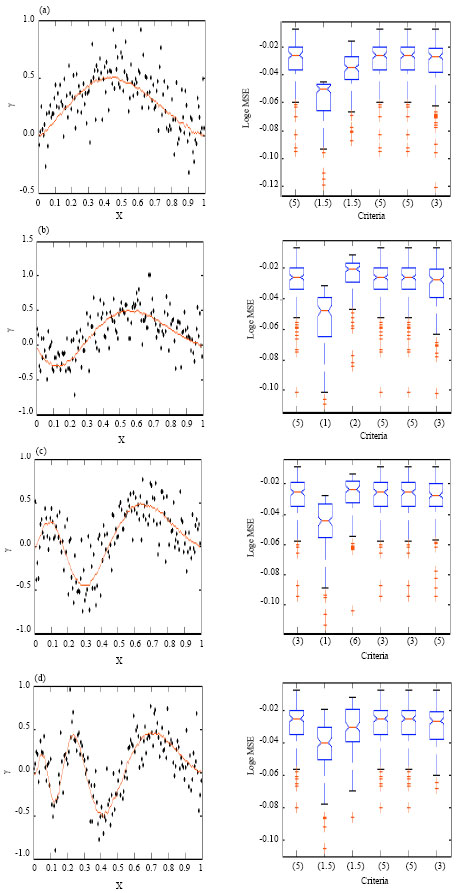
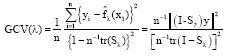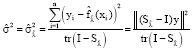Research Article
Smoothing Parameter Selection Problem in Nonparametric Regression Based on Smoothing Spline: A Simulation Study
Department of Statistics, Mugla University, 48000, Mugla, Turkey
M. Seref Tuzemen
Department of Industrial Engineering, Anadolu University, 426470, Eskisehir, Turkey