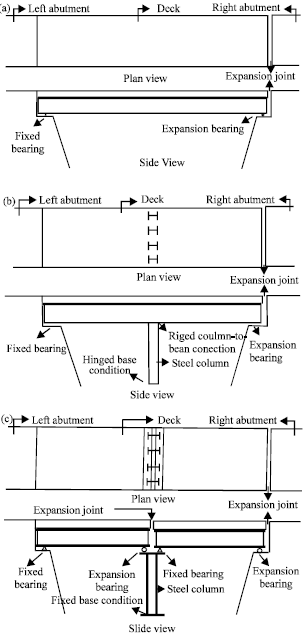
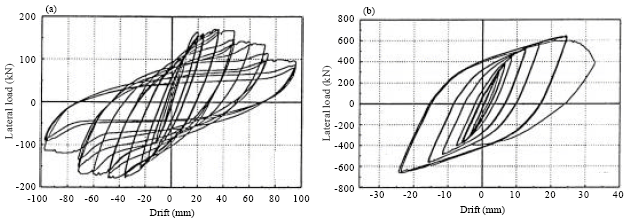
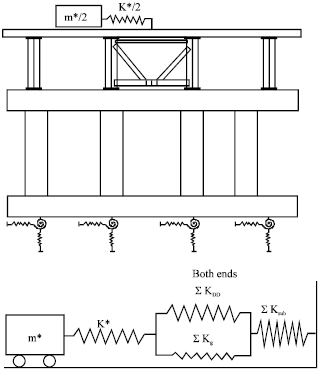
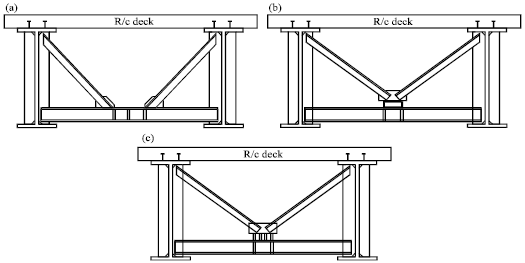
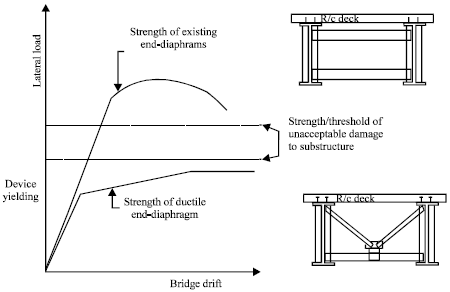
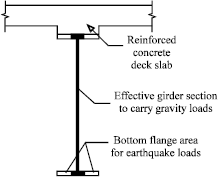
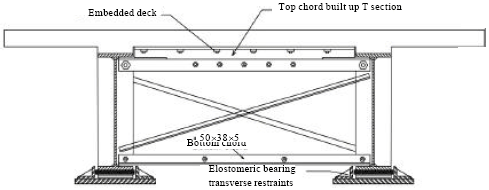
Review Article
Review on Seismic Behavior of Slab-on-girder Steel Highway Bridges
School of Civil Engineering, Engineering Campus, Universiti Sains of Malaysia, Nibong Tebal, 14300, Malaysia
Taksiah A. Majid
School of Civil Engineering, Engineering Campus, Universiti Sains of Malaysia, Nibong Tebal, 14300, Malaysia
Norazura M. Bunnoriand
School of Civil Engineering, Engineering Campus, Universiti Sains of Malaysia, Nibong Tebal, 14300, Malaysia
Amir Darvishi
Faculty of Engineering, Chaloos Branch, Islamic Azad University, Chaloos, 46615-397, Iran