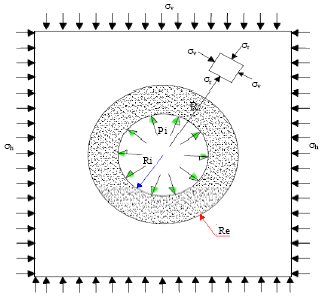
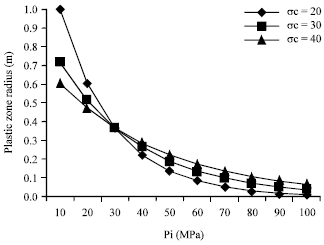
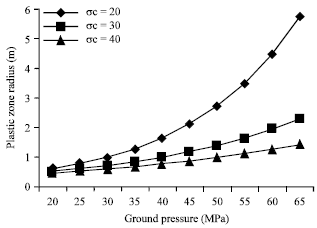
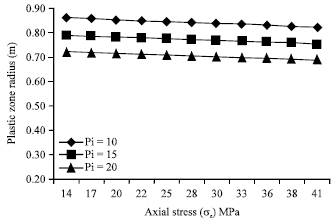
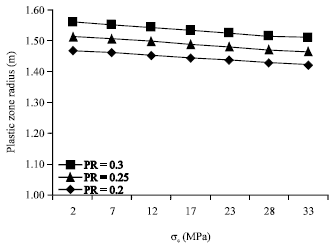
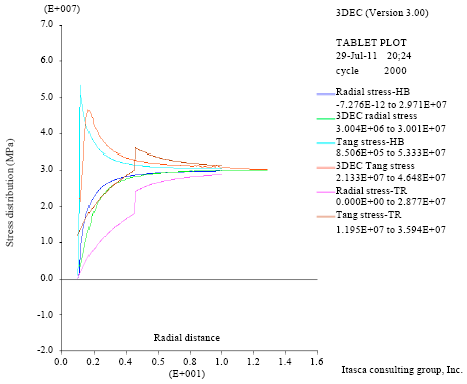
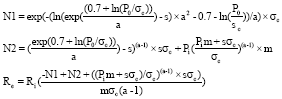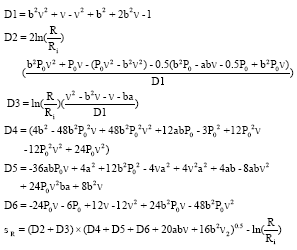Research Article
An Analytical Closed Form Solution Around Underground Openings Using Different Methods
School of Mining Engineering, Shahrood University of Technology, Shahrood, Iran
A. Elyasi
Rock Mechanics College, Tarbiat Modares University, Tehran, Iran
S. Maleki
School of Mining Engineering, Shahrood University of Technology, Shahrood, Iran
A. Fegh
School of Mining, University of Tehran, Tehran, Iran