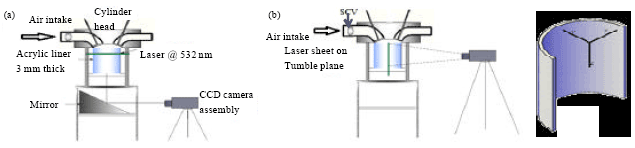
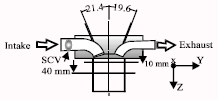
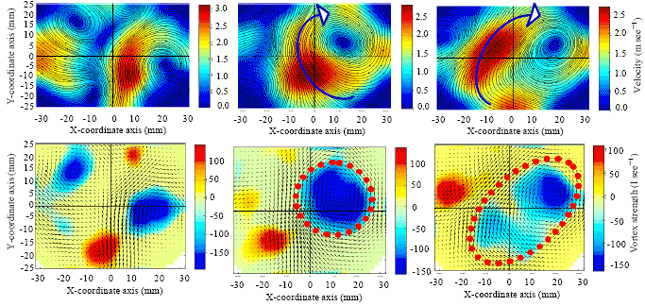
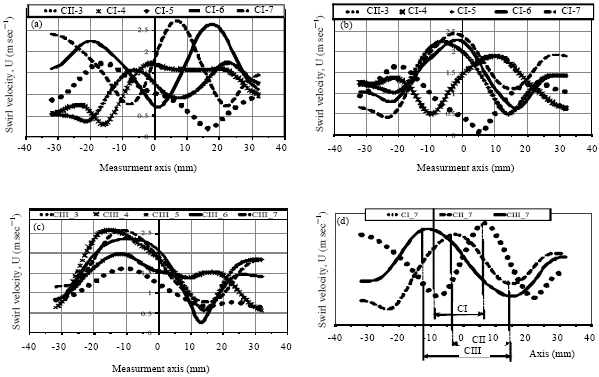
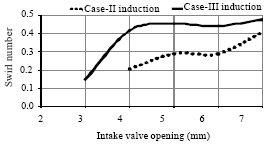
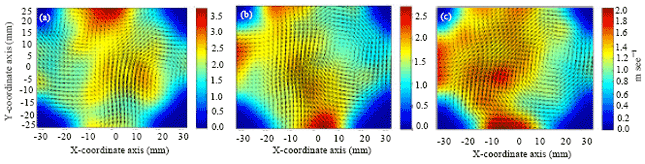
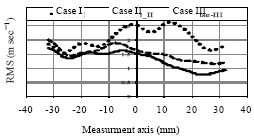
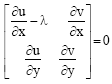Research Article
Characteristics of Induction Flow in SI Direct Injection Engine with Dual Variable Swirl Control Valve
Center for Automotive Research and Electric Mobility, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
A. Rashid A. Aziz
Center for Automotive Research and Electric Mobility, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Morgan R. Heikal
Center for Automotive Research and Electric Mobility, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia