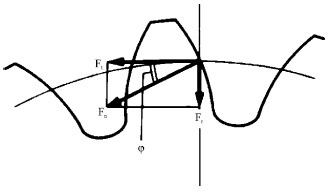
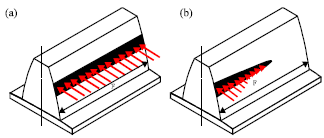
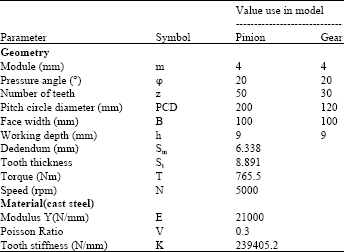
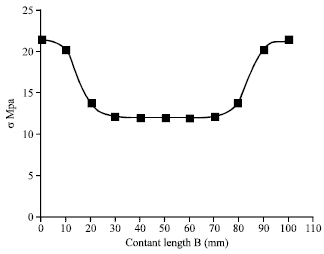
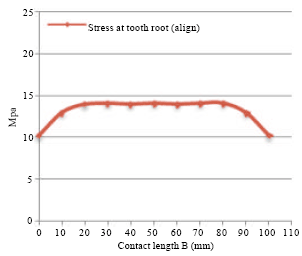
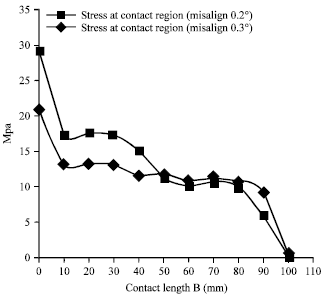
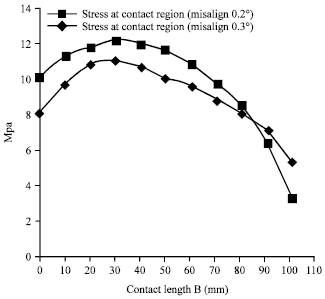
Research Article
The Stress Distribution of Gear Tooth Due to Axial Misalignment Condition
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
T.V.V.L.N. Rao
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
M. Awang
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
M.A. Khan
Pakistan Navy Engineering College, National University of Sciences and Technology, Karachi, Pakistan