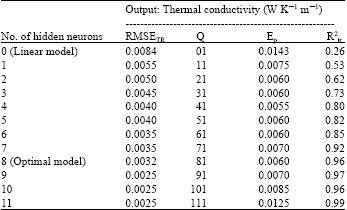
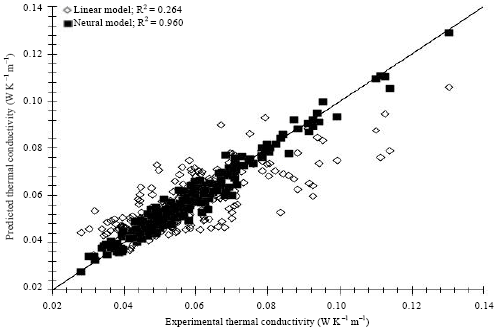
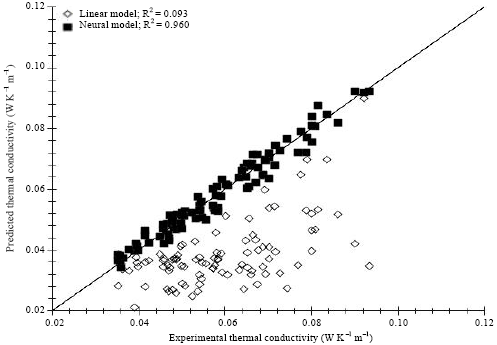
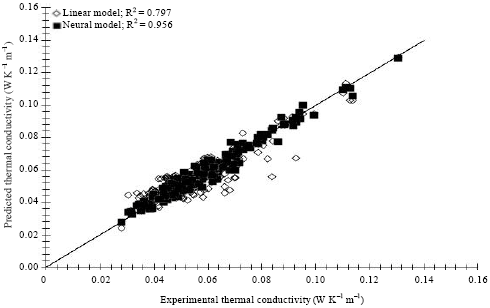
Research Article
Modeling of Thermal Conductivity of Stretch Knitted Fabrics Using an Optimal Neural Networks System
Laboratory of Study of the Thermal and Energy Systems (LESTE), National School Engineers of Monastir, University of Monastir, Avenue IBN ELJAZZAR, 5019 Monastir, Tunisia
Faten Fayala
Laboratory of Study of the Thermal and Energy Systems (LESTE), National School Engineers of Monastir, University of Monastir, Avenue IBN ELJAZZAR, 5019 Monastir, Tunisia
Abdelmajid Jemni
Laboratory of Study of the Thermal and Energy Systems (LESTE), National School Engineers of Monastir, University of Monastir, Avenue IBN ELJAZZAR, 5019 Monastir, Tunisia
Xianyi Zeng
Gemtex Research Laboratory, National School of Arts And Textiles Industries (ENSAIT), Roubaix, University North Lille of France, Avenue de l�Hermitage, Roubaix Cedex, France