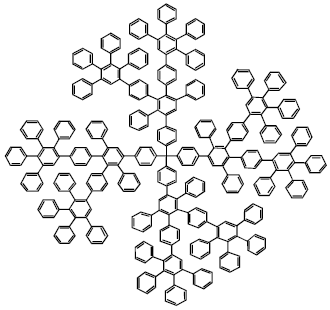
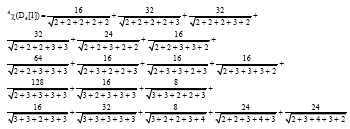
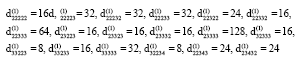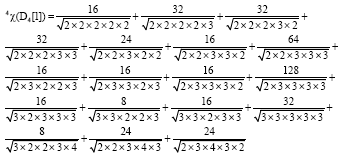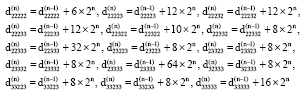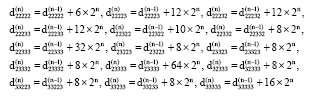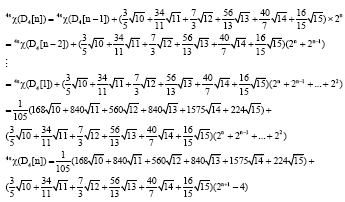Research Article
Fourth Order and Fourth Sum Connectivity Indices of Polyphenylene Dendrimers
School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Penang, Malaysia
Roslan Hasni
Department of Mathematics, Faculty of Science and Technology, Universiti Malaysia Terengganu, 21030 Kuala, Terengganu, Malaysia
Saeid Alikhani
Department of Mathematics, Yazd University, 89175-741, Yazd, Iran