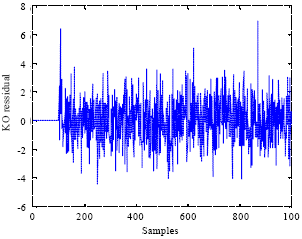
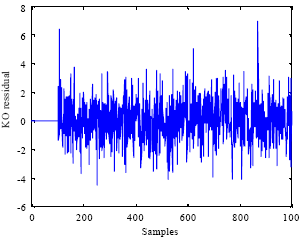
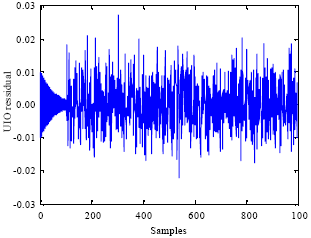
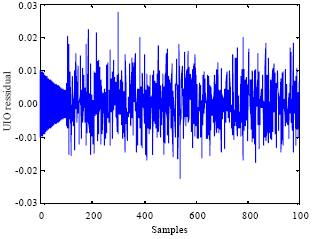
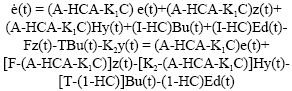Research Article
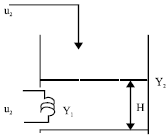
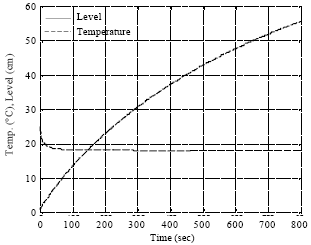
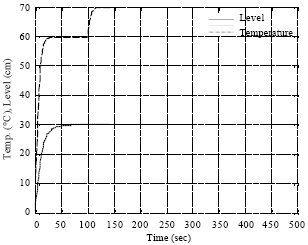
Decoupling and Soft Sensor Design for a Class of MIMO System
Department of Instrumentation and Control Systems Engineering, PSG College of Technology, Coimbatore, India
J. Kanakaraj
Department of Electrical and Electronics Engineering, PSG College of Technology, Coimbatore, India