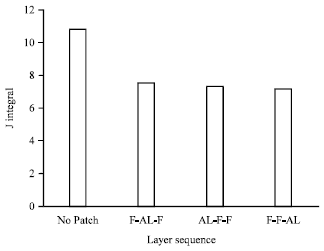
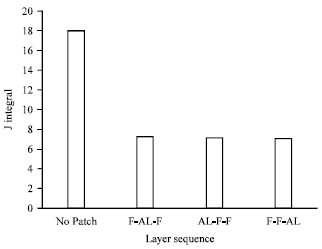
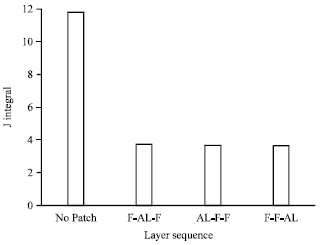
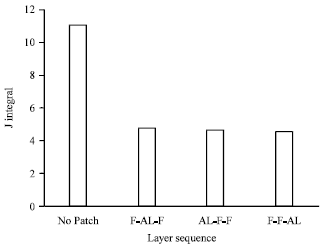
Research Article
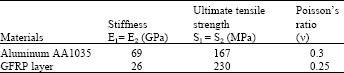
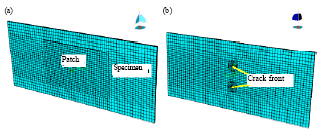
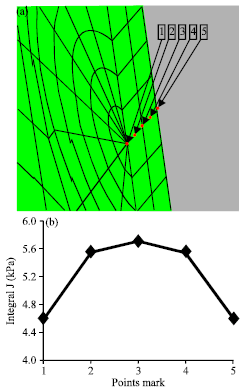
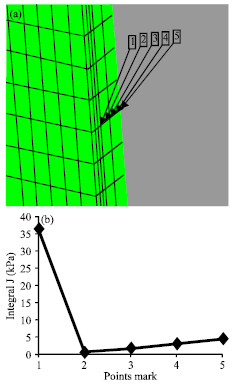
Numerical Analysis for Determination of the J Integral and Crack Opening Displacement in the Cracked Aluminum Plates Repaired with FML Composite Patches
Department of Mechanical Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran
Faramarz Ashenai Ghasemi
Department of Mechanical Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran
Ali Pourkamali Anaraki
Department of Mechanical Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran
Ahmad Fallah Rahmatabadi
Department of Mechanical Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran