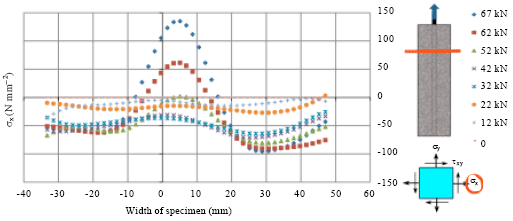
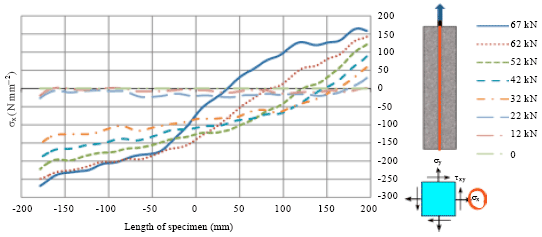
Research Article
Mapping Full-field Bond Stress Distribution on Concrete using Digital Image Correlation Results
Department of Civil Engineering, Ahar Branch, Islamic Azad University, Ahar, Iran
Redzuan Abdullah
Department of Structures and Materials, Faculty of Civil Engineering, Universiti Teknologi Malaysia, Johor, Malaysia
Mahmood Md. Tahir
Department of Structures and Materials, Faculty of Civil Engineering, Universiti Teknologi Malaysia, Johor, Malaysia