Research Article
Nonlinear Analysis of Concrete Structural Components Using Co-axial Rotating Smeared Crack Model
Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran
S. Mahdi S. Kolbadi
Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran
Masoud Heshmati
Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran
Hasan Mirzabozorg
Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran









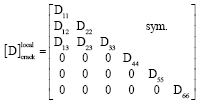
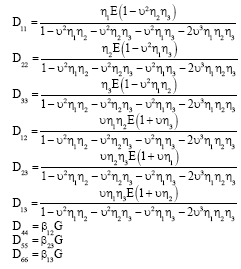
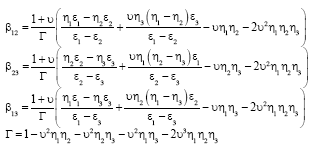

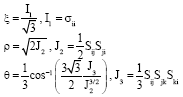
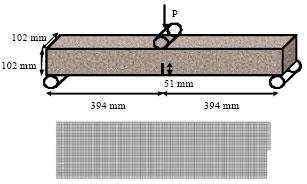
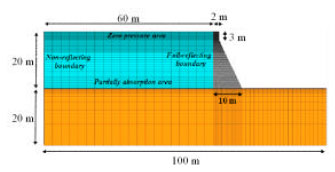



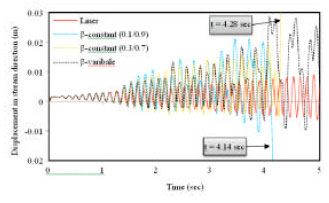
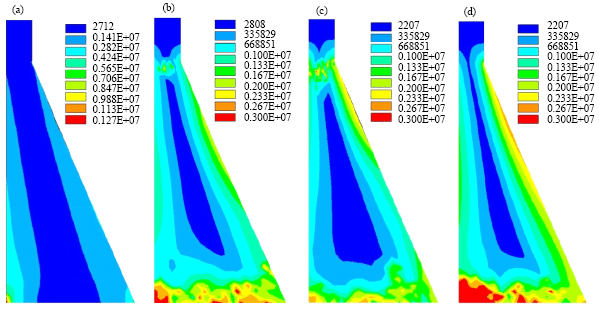
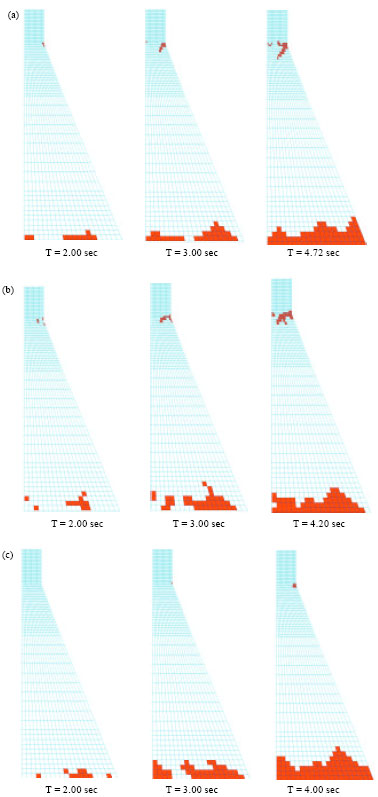
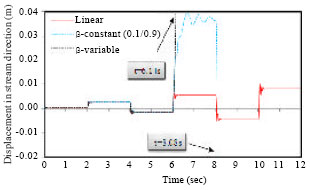
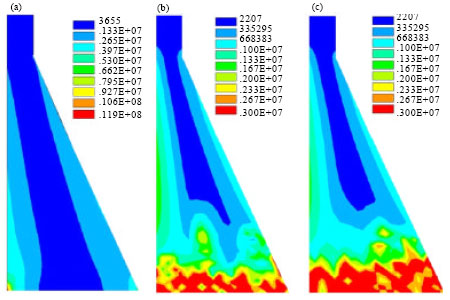
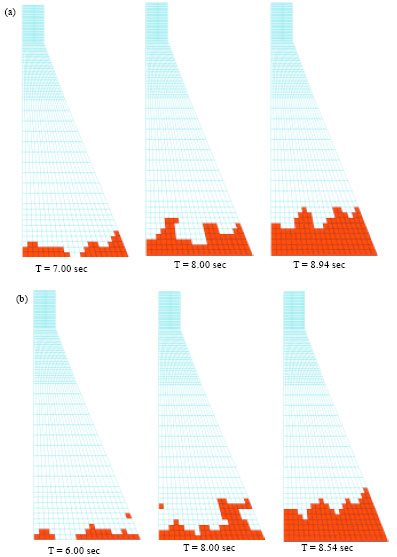
mohamad kolbadi Reply
Dear Mr. Kolbadi, Hi
I did study your paper.It is a wonderful science essay and so useful. I whishing that you and your friend reach to multifarious and great prosper in your life.
My god bless you.
Have a nice time.