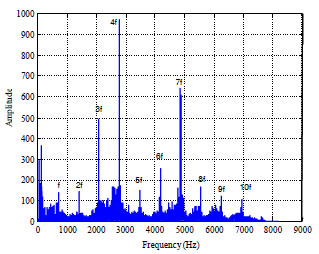
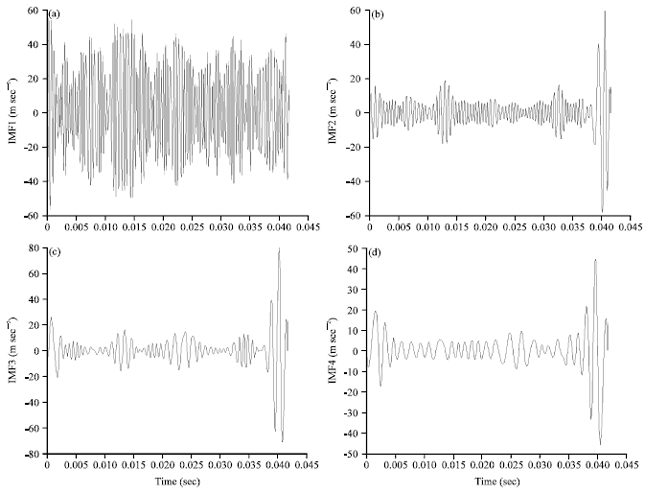
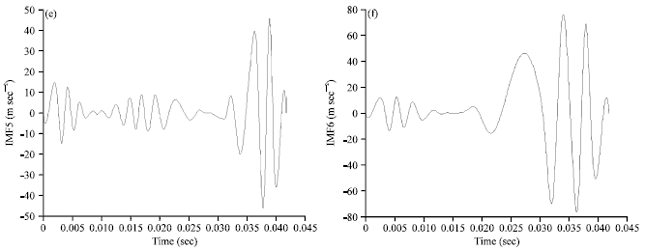
Research Article
Intelligent Fault Diagnosis via EMD Method
Department of Mechanical Engineering, Behbahan Branch, Islamic Azad University, Behbahan, Iran
Masoud Dorfeshan
Department of Mechanical Engineering, Khatam Al Anbiya University of Technology, Behbahan, Iran