Research Article
An Intelligent Mining Framework based on Rough Sets for Clustering Gene Expression Data
Department of IT, Sona College of Technology, Salem, Tamil Nadu, India
K. Ramar
Einstein College of Engineering, Tirunelveli, Tamil Nadu, India
The gene expression profile is a representation of the complex mechanism behind cancer and the changes in gene expression levels are very common in complex diseases like cancer. Microarray technology is considered as an enhancement to simultaneously observe the expression levels of thousands of genes across collections of related samples. The significant task in analyzing gene expression data is identification of co-expressed genes and the coherent gene expression pattern (Ben-Dor et al., 1999; Eisen et al., 1998).
Numerous clustering algorithms that can be applied in different fields have been proposed, analyzed and improved (Jiang et al., 2004). The conventional algorithms like k-means, hierarchical, SOM and other density based methods are very common. These algorithms have their own merits and demerits. Hemalatha and Vivekanandan (2008) have proposed an enhanced version of k-means clustering algorithm which is claimed to be parallel and distributed. Garg and Jain (2006) have done a comparison on some of the existing variations of k-mean algorithms. They have used the synthetic sets of high dimensional data as benchmark for evaluating the algorithms and have also proposed some criteria for comparison of these clustering algorithms. Ranjan and Khalil (2007) have worked with the statistical approaches in hierarchical clustering and have also done a comparison on the linkage methods which can assist us in knowing the functionalities of many genes. Vijendra (2011) has presented a detailed review of various subspace and density based clustering algorithms, their efficiencies and inefficiencies on different data sets. Zhou et al. (2007) have proposed a Join-Prune algorithm that shows momentous gain in runtime and quality.
Recently a series of pattern based clustering methods have been proposed to capture coherence exhibited by subset of genes over subset of conditions. An increasing number of biclustering algorithms have also been proposed for identifying gene patterns (Madeira and Oliveira, 2004). An iterative co-clustering algorithm that mainly concentrates on user defined constraints and minimizes the sum squared residue was addressed in (Pensa and Boulicaut, 2008). k-biclusters clustering (KBC Algorithm) suggested by Tsai and Chiu (2010) aims in minimizing the dissimilarities between genes and bicluster centers thereby minimizing the residue within the clusters. It also tries to involve as many conditions as possible in each iteration of clustering. Of late the concept of Rough sets has also been introduced into clustering and a few clustering algorithms have been developed based on rough set theory (Prelic et al., 2006; Emilyn and Ramar, 2010; Shi, 2009). Arora et al. (2009) have proposed an integrated approach for filtering all the non-reduct attributes using rough set theory. A Rough Overlapping Biclustering (ROB) algorithm proposed by Wang et al. (2007) also works on the framework of generalized rough sets.
The principal aim of this work is in developing an algorithm based on intelligent rough clustering techniques which will efficiently mine co-regulated genes from gene expression dataset by removing the irrelevant dimensions in a high dimensional space and obtain appropriate meaningful clusters.
In this study, we have proposed a framework for mining co-regulated genes from gene expression dataset. The framework is composed of three sections: 1) a preprocessing step to refine the data so that all the biclusters generated would be meaningful (2) a procedure to determine the possible number of biclusters and (3) a biclustering algorithm based on rough sets. The structure of the proposed framework is shown in Fig. 1.
Preprocessing of data: In gene expression matrix, the intensity values of different genes vary widely. This difference may be due to the influence of different gene dimensions. In order to handle this variation, the values have to be normalized. Normalization is done using Eq. 1:
| (1) |
Where:
where, e'ij represents normalized intensity value for gene i under condition j and eij denotes the original intensity value for gene i under condition j, m is the number of conditions and μi is the mean of the intensity value.
Some genes in the gene expression matrix do not react much to the experimental conditions and so show very less significance in biclustering the data. These genes named as 'flat genes' should be removed to provide good quality biclusters. For this, we follow the method proposed by Tang et al. (2001). After normalization each gene vector with j conditions can be represented as gi = (e'i1, e'i2,...e'ij ). A vector-cosine can be used between each gene vector and a pre-defined stable pattern H = (h1, h2,.....hj) to determine the variation in the gene intensity values among samples:
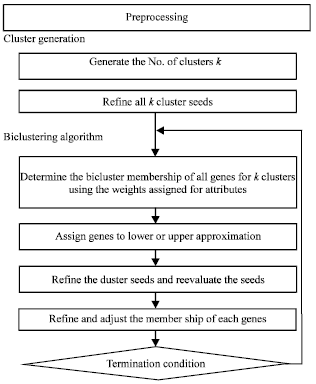 | |
| Fig. 1: | The structure of rough bi clustering algorithm (ROBICA) |
If the value of the cosine-vector is close to 1, then both the vector are more similar. A threshold value can be chosen and genes which have θ values more than the threshold δ (those that are more similar to the pattern) can be removed. The data is now considered to be ready for clustering.
Procedure to detect possible number of biclusters: Biclustering is the problem of finding a subset of the vectors (genes) that express a similar pattern over a subset of the dimensions. The problem requires grouping the vectors and the dimensions at the same time, thus, the name “biclustering”. In our algorithm we define a bicluster based on the Pearson’s correlation coefficient (Bhattacharya and De, 2009) as the similarity measure. Pearson’s correlation coefficient for measuring the similarity between two genes (xi, xj) is given as:
| (2) |
The procedure for finding the possible number of biclusters is shown in Fig. 2. Initially, all conditions are considered in the condition set for any pair of genes. Then the algorithm finds out the condition which when eliminated gives the maximum correlation. That condition is eliminated from the condition set and repeat this step until you have not less than some specified number of conditions in the condition set. Repeat step B for all genes and add them to this cluster. When there are no more genes to be added increment the cluster count by 1. Repeat the entire process (steps B and C) for the next two pair of genes until there is no more pair to be considered. The variable count will give the possible number of biclusters.
Rough biclustering algorithm (ROBICA): The proposed new algorithm, Rough Biclustering Algorithm (ROBICA), clusters genes based on rough set theory. The main advantage of this method is that it not only places each gene in the corresponding bicluster but also assigns a weight for different conditions depending upon the significance of the condition in the bicluster. Genes can get expressed in two are more clusters i.e. overlapping of genes are possible. The membership matrix, weight matrix and the center matrix are calculated similar to that of SCAD algorithm (Frigui and Nasraoui, 2004).
The equation for finding the membership matrix U given W and O is presented as:
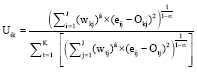 | (3) |
where, 1≤i≤I and 1≤k≤K. The equation for finding the bicluster centroids given W and U can be shown as:
| (4) |
And finally, the equation for calculating and updating the weights for the J conditions can be given as:
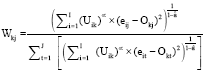 | (5) |
 | |
| Fig. 2: | Algorithm for detecting the number of bicluster, The similarity between any two genes Sim (gi, gj) is calculated using correlation coefficient, This algorithm returns the possible number of biclusters as output |
 | |
| Fig. 3: | Pseudo code of ROBICA, The algorithm generates both upper and lower approximations for each cluster using the values of the membership matrix |
Initially, the values for W are generated randomly whereas the center values O for the k biclusters are got by finding the mean of all the genes assigned to the biclusters in the above procedure. Afterwards, the ROBICA algorithm repeats to calculate the membership matrix, weight matrix and centers using Eq. 3-5 until all k bicluster centers in O remain the same without being changed. The dissimilarity between gene Gi and object center Ok is defined as:
| (6) |
where, eij is the expression level of gene Gi in condition Cj and Wjk gives the weight assigned for all j conditions in k biclusters. The pseudo-code of the ROBICA is illustrated in Fig. 3. Through the ROBICA algorithm, the genes belonging to the bicluster can be identified based on the elements uik for I = 1,…, I in U. If the membership values fall above the threshold λ, the gene is put in the lower approximation. If the value is between λ and ù , then the gene is placed in the upper approximation. If the value falls below ù , the gene is not in the bicluster. Similarly, the conditions used for the bicluster can be identified based on the elements wjk for j = 1,…, J in W. If wkj = 1/J in W, then the experimental condition belongs to the bicluster Bk. If wkj<1/J, the condition does not belong to Bk. Since, we decide the placement of a gene in a bicluster based on the membership values, there are high possibilities of placing a gene in more than one bicluster. This is how this algorithm allows overlapping of biclusters. Therefore, the goal of biclustering has been achieved by the ROBICA algorithm.
The algorithm generates the membership matrix based on the rough set theory (Pawlak, 1982). The lower approximation is a subset of the upper approximation. The members (genes or conditions) of the lower approximation belong to and only belong to the bicluster. However, the members of the upper approximation may belong to more than one biclusters. The boundary region between the lower and upper approximation forms an overlapping part among corresponding biclusters. Therefore, it is anticipated that lower and upper approximation resulting directly from expression data would better capture the overlapping feature among the co-regulated genes.
The performance of the proposed ROBICA Algorithm was experimented with two different sets of data. Initially the algorithm was experimented with yeast expression data downloaded from http://faculty.washington.edu/kayee/model. The data set is 384x17 matrix. A total of 384 genes were clustered based on 17 experimental conditions. Next the algorithm was experimented with colon cancer data set which contains expression levels of 2000 genes taken from 62 different samples out of which 50 genes where chosen across all 62 samples.
As most clustering methods, the proposed ROBICA uses several parameter to approximate the optimal solution. During data pre-processing procedure, we choose the threshold for the vector-cosine δ to be 0.7 (Table 1). We then remove genes with vector-cosine higher than that threshold.
| Table 1: | Parameter settings |
 | |
| The table gives the values for the parameters used in the different stages of the algorithm. During the preprocessing step, we use the threshold δ for the vector cosine. The second stage uses a correlation coefficient θ. In the third stage we use the parameters α and β for generating the membership matrix and the parameters λ and ω for finding the lower and upper boundaries of the biclusters | |
The intensity values of 802 genes were found to vary little across the conditions and so were removed from 2884 genes.
After preprocessing, we move on to the generation of the initial biclusters where we use a correlation threshold θ. The selection of optimum correlation threshold value by varying correlation threshold between 0 and 1 and judging each biclustering result takes huge amount of time. Based on the study by Allocco et al. (2004), which states that two genes having expression profile correlation >0.84 have more than 50% chance of being bounded by the same transcription factor, we have chosen the threshold value to be 0.85. Further, two parameters α and β have to be assigned for the ROBICA algorithm. The values for the pair (α, β) = (2,1.5) is considered for this algorithm.
The algorithm was experimented for different values of λ and ω. The cluster profile plot in Fig. 4 shows the biclusters generated by ROBICA for colon cancer dataset. Figure 4 represents six different biclusters generated on colon cancer data set by the proposed ROBICA algorithm. Each subdivision (Fig. 4a-f) shows the expression levels of genes that are grouped in separate clusters. In all rough clustering algorithms, the number of objects in the boundary region depends on the value of the threshold λ. It has been noted for our algorithm that the number of genes in the boundary region decreases as the value of λ becomes > 0.8 and ù becomes >0.5. When the threshold value becomes smaller, the number of genes in the boundary region also increases. The accuracy of the algorithm for different values of λ and ω is shown in Fig. 5.
Performance comparison: The performance of ROBICA is compared with a few biclustering algorithms like KBC (Tsai and Chiu, 2010), SCAD(Frigui and Nasraoui, 2004), ROB (Wang et al., 2007), CC (Cheng and Church, 2000), Rough k-means (Pawan and West, 2004), RCGED (Emilyn and Ramar, 2011), BCCA (Bhattacharya and De, 2009), Bimax (Prelic et al., 2006) for its accuracy.
 | |
| Fig. 4(a-f): | Colon cancer data set clustered using ROBICA. Cluster profile plot (with the x-axis representing the genes and the y-axis representing the expression levels) showing the different biclusters generated using ROBICA, (a) Genes grouped into Cluster 1 and their expression levels, (b) Genes grouped into Cluster 2 and their expression levels, (c) Genes grouped into Cluster 3 and their expression levels, (d) Genes grouped into Cluster 4 and their expression levels, (e) Genes grouped into Cluster 5 and their expression levels and (f) Genes grouped into Cluster 6 and their expression levels |
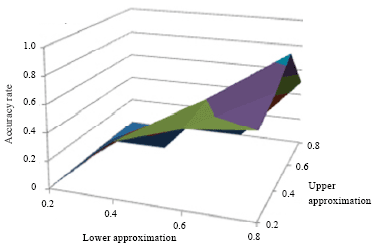 | |
| Fig. 5: | Accuracy rate of ROBICA for different values of λ and ω figure shows a maximum accuracy for the value (0.8, 0.5) |
| Table 2: | Accuracy comparison for different algorithms for both yeast and colon cancer data sets |
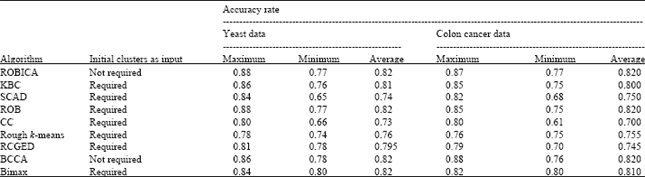 | |
| ROBICA: Rough biclustering algorithm, KBC: k-biclusters clustering, SCAD: Simultaneous clustering and attribute discrimination algorithm, ROB: Rough overlapping biclustering, CC: Cheng and Church (2000), RCGED: Rough clustering of gene expression data, BCCA: Bi-correlation clustering algorithm, Bimax: Binary inclusion-maximal biclustering algorithm | |
All of these clustering algorithms except BCCA require the number of clusters to be specified as input. This is not appreciable because small no of cluster centers tend to generate few large clusters and large number of cluster centers generate large number of small clusters. As this may not be accurate, we have come out with a procedure to find out the possible number of biclusters based on the correlation of the genes with one another. These biclusters are refined further in the ROBICA algorithm. Moreover in our method, each and every bicluster is defined with a lower and an upper boundary based on the rough set theory. By doing this, we allow overlapping of biclusters. Gene in the upper boundary of one bicluster can also fall into a boundary of a different bicluster. The maximum and minimum accuracy rate of ROBICA algorithm is compared with the other methods for both the yeast and colon cancer datasets (Table 2).
In this article, we propose a novel approach based on rough set theory for clustering gene expression data. It is based on the idea that a group of genes can be clustered together if they exhibit a similar pattern over a subset on experimental conditions. Consequently, we cluster the genes based on the weights assigned to the experimental conditions. A rough set based biclustering algorithm is utilized in the clustering process. The number of clusters in the gene expression data is automatically determined in this biclustering algorithm. We present here, the theoretical understanding, analysis and results of the ROBICA algorithm. Our algorithm proves to be robust as it handles noisy data during the preprocessing step. Then it proves to be intelligent when is automatically detect the possible number of biclusters. It also proves to be a novel method as it allows overlapping of biclusters and also finds the lower and upper boundaries for each bicluster.