Research Article
A New Mixed Negative Binomial Distribution
Department of Statistics, Faculty of Science, Kasetsart University, Phahonyothin Road, Jathujak, Bangkok, Thailand
Winai Bodhisuwan
Department of Statistics, Faculty of Science, Kasetsart University, Phahonyothin Road, Jathujak, Bangkok, Thailand
Panlop Zeephongsekul
School of Mathematics and Geospatial, Faculty of Applied Science, RMIT University, Melbourne, VIC 3000, Australia










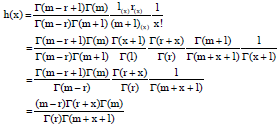
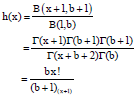


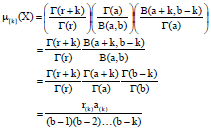
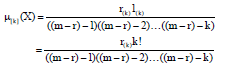
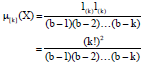
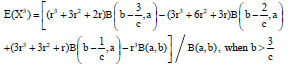
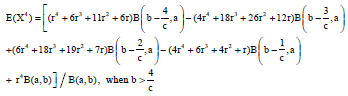

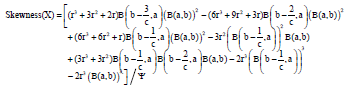
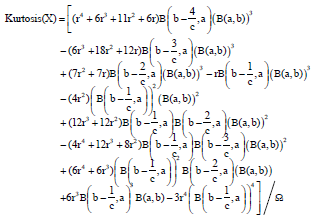

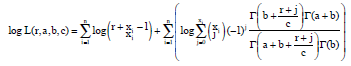
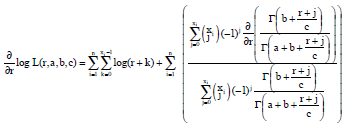

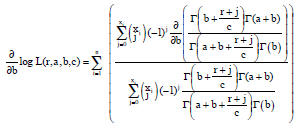

kolawole Sunday Reply
Sir,
This is an interesting and educative article for somebody like me. I have decided to use it as training manual which I believe will improve my understanding of distribution theory.
Please, I need your assistance in the area of the application to my dataset. Can I get the code in R or which package will help me out? It is very important to me because I have used different methods for my data which have not given me better model.Please, assist me. Thank you indeed.