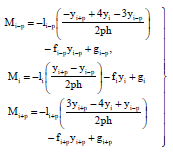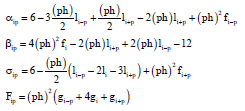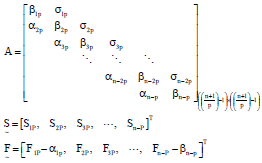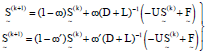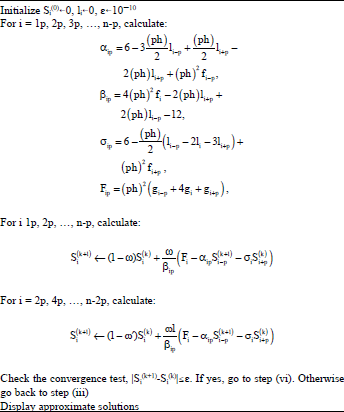Research Article
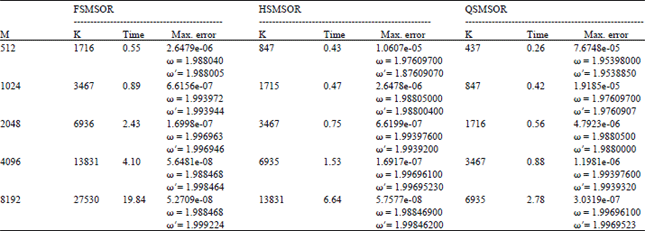
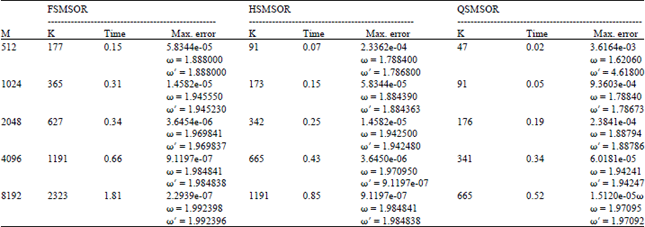
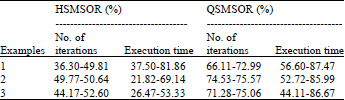
Quarter-sweep Modified SOR Iterative Algorithm and Cubic Spline Basis for the Solution of Second Order Two-point Boundary Value Problems
Mathematics with Economics Programme, School of Science and Technology, Universiti Malaysia Sabah, 88400 Kota Kinabalu, Sabah, Malaysia
J. Sulaiman
Mathematics with Economics Programme, School of Science and Technology, Universiti Malaysia Sabah, 88400 Kota Kinabalu, Sabah, Malaysia