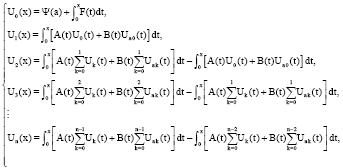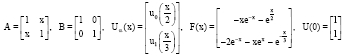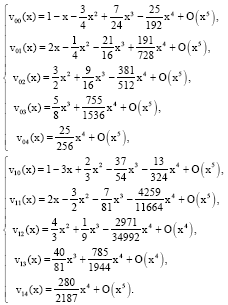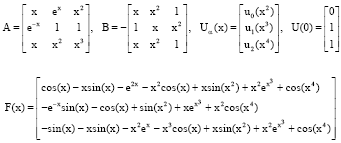Research Article
A Telescoping Numerical Scheme for the Solution of Retarded Delay Differential Systems
Department of Mathemetics, Khomeini Shahr Branch, Islamic Azad University, Isfhan, Iran
S. Karimi
Department of Mathemetics, Khomeini Shahr Branch, Islamic Azad University, Isfhan, Iran
J. Sedighi
Department of Mathemetics, Khomeini Shahr Branch, Islamic Azad University, Isfhan, Iran