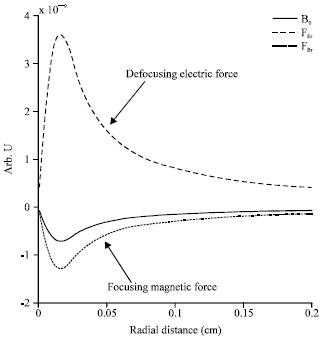
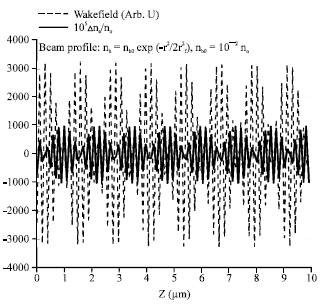
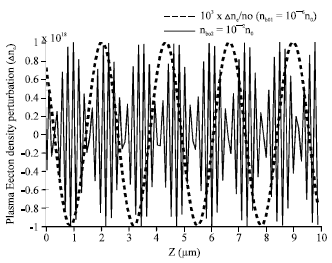
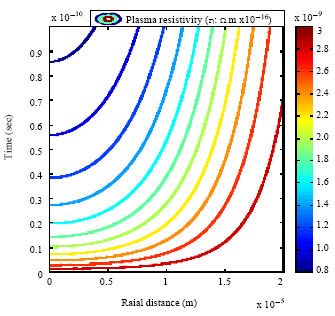
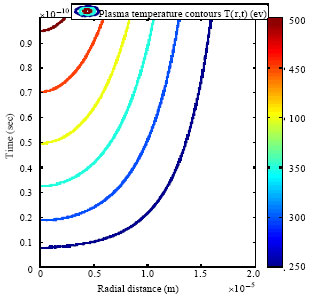
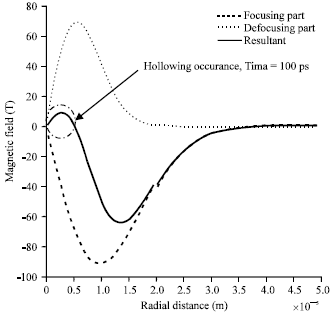
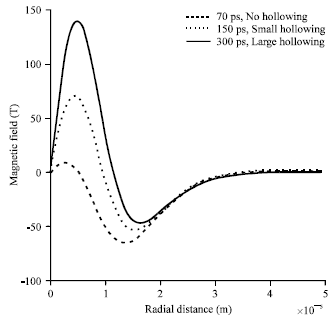
Research Article
Self Generated Fields Effects of Fast Electrons Beam on Plasma and Beam Characteristics
Department of Physics, Mazandaran University, P. O. Box 47415-416, Babolsar, Iran
S.F. Ghazizadeh
Department of Physics, Tehran Payam-e-Noor University, Tehran, Iran